Capítulo 3: Machine Learning#

O que é Inteligência Artificial?#
A Inteligência Artificial (IA) é uma área multidisciplinar da ciência da computação voltada para o desenvolvimento de sistemas capazes de realizar tarefas que, até então, exigiam inteligência humana. Essas tarefas incluem aprendizado, raciocínio, resolução de problemas, percepção sensorial (como visão e audição) e compreensão da linguagem natural.
Contexto Histórico#
O desenvolvimento moderno da IA teve início no século XX, impulsionado por avanços nas áreas de matemática, ciência da computação, neurociência e, posteriormente, estatística e engenharia.
1950: Alan Turing, matemático britânico conhecido por seu papel fundamental na quebra do código Enigma durante a Segunda Guerra Mundial, propôs o Teste de Turing como um critério para avaliar se uma máquina pode exibir comportamento inteligente indistinguível do humano.
1956: A Conferência de Dartmouth, organizada por John McCarthy, Marvin Minsky, Claude Shannon e Nathaniel Rochester, é considerada o marco inicial da pesquisa formal em IA. Nela, cunhou-se o termo “Inteligência Artificial”.
Décadas de 1960 e 1970: Houve avanços significativos em áreas como resolução de problemas e jogos. Programas notáveis incluem o ELIZA, que simulava um psicoterapeuta por meio de regras simples de linguagem, e o SHRDLU, que interpretava comandos em linguagem natural para manipular objetos em um mundo virtual.
Décadas de 1980 e 1990: O interesse por redes neurais ressurgiu, impulsionado por novos algoritmos de aprendizado e pelo aumento da capacidade de processamento computacional. Nesse período, os sistemas especialistas ganharam destaque, como o MYCIN, desenvolvido para auxiliar no diagnóstico de doenças infecciosas.
2012: O artigo “ImageNet Classification with Deep Convolutional Neural Networks”, publicado por Alex Krizhevsky, Ilya Sutskever e Geoffrey Hinton, introduziu a arquitetura conhecida como AlexNet. Essa rede neural convolucional profunda venceu a competição ImageNet Large Scale Visual Recognition Challenge (ILSVRC) de 2012, reduzindo significativamente a taxa de erro em comparação com os métodos anteriores. O sucesso da AlexNet demonstrou o potencial das redes neurais profundas treinadas com GPUs e técnicas como ReLU, dropout e data augmentation, marcando o início da era moderna do deep learning.
2000 até o presente: A IA passou por uma nova revolução, impulsionada por três fatores principais: maior disponibilidade de grandes volumes de dados (big data), avanços nos algoritmos de aprendizado de máquina, especialmente aprendizado profundo (deep learning), e o acesso a maior poder computacional (como GPUs e, mais recentemente, TPUs). Essa fase resultou em avanços expressivos em reconhecimento de voz, visão computacional, tradução automática e sistemas de recomendação, além da popularização de assistentes virtuais e modelos de linguagem como o ChatGPT.
Redes Generativas e Agentes Autônomos: A Nova Fronteira da IA#
As redes generativas representam um dos desenvolvimentos mais impactantes no campo recente. Goodfellow et al. (2014) introduziram as Generative Adversarial Networks (GANs), cujos fundamentos são detalhados no Dive into Deep Learning. Paralelamente, Variational Autoencoders (VAEs) Kingma & Welling, 2013 e os mais recentes Diffusion Models Ho et al., 2020 revolucionaram a geração de conteúdo multimídia.
Um avanço significativo recente vem do trabalho da DeepSeek com seu paper sobre Large Language Models DeepSeek, 2023, que demonstra técnicas inovadoras de treinamento em escala e alinhamento de modelos generativos. Essa abordagem permite a criação de agentes de IA mais robustos e capazes de raciocínio complexo.
Os Agentes Autônomos emergiram como paradigma promissor, combinando modelos de linguagem com capacidades de planejamento e execução de tarefas. Trabalhos como AutoGPT e AgentBench demonstram como esses sistemas podem operar de forma autônoma, aprendendo com o ambiente e tomando decisões sequenciais.
A convergência entre modelos generativos e agentes autônomos está criando sistemas capazes não apenas de gerar conteúdo, mas de planejar e executar fluxos complexos de trabalho. Essa sinergia, exemplificada em projetos como Microsoft’s AutoGen, aponta para um futuro onde assistentes de IA poderão gerenciar projetos completos de forma autônoma.
A evolução contínua dessas tecnologias, impulsionada por avanços em arquiteturas neurais e técnicas de treinamento, está redefinindo radicalmente nosso conceito de automação inteligente e criatividade computacional.
Fundamentos Matemáticos#
Antes de mergulharmos no universo das redes neurais artificiais, é fundamental construir uma base sólida em dois pilares da matemática: álgebra linear e cálculo. Essas áreas nos ajudam a entender como os modelos processam, transformam e aprendem a partir dos dados.
Vamos explorar os principais conceitos de álgebra linear com exemplos práticos em Python, utilizando a biblioteca NumPy — uma ferramenta poderosa e amplamente utilizada em ciência de dados e inteligência artificial.
Álgebra Linear#
A álgebra linear estuda estruturas como escalars, vetores, matrizes e tensores — elementos essenciais para o funcionamento interno das redes neurais. A seguir, veremos cada um desses conceitos acompanhados de suas expressões matemáticas e exemplos computacionais.
Escalares#
Um escalar é simplesmente um número real, denotado por:
Onde \(a\) representa qualquer número real, como 3.5. Esse valor pode, por exemplo, representar um parâmetro ajustável de uma rede neural.
import numpy as np
# Exemplo de escalar
escalar = 3.5
print(escalar)
Saída do Código
3.5
Vetores#
Um vetor é uma sequência ordenada de números reais. Ele é representado como:
Onde cada \(v_i \in \mathbb{R}\) é um componente do vetor \(\mathbf{v}\), que pode conter, por exemplo, atributos como altura, peso e idade.
# Exemplo de vetor
vetor = np.array([1.0, 2.0, 3.0])
print(vetor)
Saída do Código
[1. 2. 3.]
Matrizes#
Uma matriz é uma grade de números organizada em linhas e colunas, representada por:
Onde \(m_{ij}\) representa o elemento da linha \(i\) e coluna \(j\). Matrizes são muito úteis para representar conjuntos de dados ou os pesos entre camadas de uma rede.
# Exemplo de matriz
matriz = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(matriz)
Saída do Código
[[1 2 3]
[4 5 6]
[7 8 9]]
Tensores#
Um tensor é uma generalização de vetores e matrizes para mais de duas dimensões. Um tensor 3D, por exemplo, pode ser representado como:
Onde \(d_1\), \(d_2\), \(d_3\) representam as dimensões do tensor (como altura, largura e canais de cor no caso de uma imagem RGB).
# Exemplo de tensor 3D
tensor = np.random.rand(3, 3, 3)
print(tensor)
Saída (valores aleatórios):
[[[0.86 0.68 0.33]
[0.77 0.42 0.90]
[0.22 0.35 0.75]]
[[0.96 0.17 0.39]
[0.34 0.67 0.72]
[0.91 0.59 0.74]]
[[0.05 0.37 0.93]
[0.32 0.25 0.69]
[0.02 0.27 0.30]]]
Resumo Visual#
Conceito |
Representação Matemática |
Exemplo em Python |
Dimensão |
|---|---|---|---|
Escalar |
\(a \in \mathbb{R}\) |
|
0D |
Vetor |
\(\mathbf{v} \in \mathbb{R}^n\) |
|
1D |
Matriz |
\(\mathbf{M} \in \mathbb{R}^{m \times n}\) |
|
2D |
Tensor |
\(\mathcal{T} \in \mathbb{R}^{d_1 \times d_2 \times \cdots}\) |
|
3D+ |
Operações entre Escalares, Vetores e Matrizes#
Produto Interno (Produto Escalar)#
O produto interno é amplamente usado no cálculo da ativação de neurônios em redes neurais.
Aplicação prática:
Cálculo da saída de um neurônio na regressão linear.
Similaridade entre vetores de características (por exemplo, em embeddings de imagens ou textos).
Matematicamente, para dois vetores \( \mathbf{a} = [a_1, a_2, \ldots, a_n] \) e \( \mathbf{b} = [b_1, b_2, \ldots, b_n] \), ambos com \(n\) componentes reais:
Ou seja, somamos o produto dos elementos correspondentes de cada vetor.
# Produto Interno (equivalente a np.dot para vetores 1D)
vetor1 = np.array([1, 2, 3])
vetor2 = np.array([4, 5, 6])
produto_interno = vetor1 @ vetor2 # operador @ equivale a np.dot aqui
print(produto_interno)
# Produto elemento a elemento (Hadamard)
produto_elementwise = vetor1 * vetor2
print(produto_elementwise)
Saída do Código
32
[ 4 10 18]
Multiplicação Matriz-Vetor#
Usada para calcular a saída de uma camada densa (fully connected) em redes neurais.
Aplicação prática:
Propagação de sinais em redes feedforward.
Transformações lineares em imagens (ex: escala de brilho ou contraste).
Seja \(\mathbf{A} \in \mathbb{R}^{m \times n}\) uma matriz com \(m\) linhas e \(n\) colunas, e \(\mathbf{x} \in \mathbb{R}^n\) um vetor com \(n\) elementos. O produto resulta em um vetor \(\mathbf{y} \in \mathbb{R}^m\):
Onde cada elemento de \(\mathbf{y}\) é obtido por um produto interno entre as linhas de \(\mathbf{A}\) e o vetor \(\mathbf{x}\).
# Multiplicação Matriz-Vetor (np.dot e @ são equivalentes aqui)
matriz = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
vetor = np.array([1, 2, 3])
resultado = matriz @ vetor # mais legível que np.dot para produto linear
print(resultado)
# Produto elemento a elemento não é válido aqui: erro se tentar matriz * vetor
Saída do Código
[14 32 50]
Multiplicação Matriz-Matriz#
A multiplicação de duas matrizes resulta em uma nova matriz. Essa operação é essencial em modelos de machine learning para processar lotes de dados e compor camadas de redes neurais.
Aplicação prática:
Propagação de múltiplas amostras ao mesmo tempo (minibatches).
Implementação eficiente de camadas densas e convolucionais.
Seja \(\mathbf{A} \in \mathbb{R}^{m \times n}\) e \(\mathbf{B} \in \mathbb{R}^{n \times p}\). O produto \(\mathbf{C} = \mathbf{A} \mathbf{B}\) resulta em uma nova matriz \(\mathbf{C} \in \mathbb{R}^{m \times p}\), onde:
\(m\) = número de linhas de \(\mathbf{A}\)
\(n\) = número de colunas de \(\mathbf{A}\) = número de linhas de \(\mathbf{B}\)
\(p\) = número de colunas de \(\mathbf{B}\)
⚠️ Importante: Para que a multiplicação seja válida, o número de colunas de \(\mathbf{A}\) deve ser igual ao número de linhas de \(\mathbf{B}\).
# Multiplicação Matriz-Matriz (np.dot e @ são equivalentes para 2D)
matriz1 = np.array([[1, 2], [3, 4], [5, 6]]) # 3x2
matriz2 = np.array([[7, 8], [9, 10]]) # 2x2
resultado = matriz1 @ matriz2 # mais claro que np.dot para 2D
print(resultado)
# Produto elemento a elemento (Hadamard) só pode ser feito entre matrizes com mesma forma
produto_elementwise = matriz1 * matriz1 # Exemplo: 3x2 * 3x2
print(produto_elementwise)
Saída do Código
[[ 25 28]
[ 57 64]
[ 89 100]]
[[ 1 4]
[ 9 16]
[25 36]]
Transposição de Matrizes#
A transposição inverte as dimensões de uma matriz, trocando linhas por colunas.
Aplicação prática:
Alinhamento de pesos e entradas.
Inversão de filtros em convoluções transpostas (usadas em redes geradoras, como GANs).
Seja \(\mathbf{A} \in \mathbb{R}^{m \times n}\), a transposta \(\mathbf{A}^\top\) é:
# Transposição de Matriz
matriz = np.array([[1, 2, 3], [4, 5, 6]])
matriz_transposta = matriz.T
print(matriz_transposta)
Saída do Código
[[1 4]
[2 5]
[3 6]]
Calculando Normas de Vetores: L1 e L2#
As normas de vetores medem o “tamanho” ou a “magnitude” de um vetor no espaço. Duas das normas mais utilizadas são a norma L1 e a norma L2 (euclidiana).
A Norma L1 é a soma dos valores absolutos dos componentes de um vetor:
Aplicação prática:
Regularização L1, que incentiva esparsidade nos coeficientes de modelos.
Métricas de distância em espaços de alta dimensão, como a “manhattan distance”.
# Norma L1
vetor = np.array([1, 2, 3])
norma_l1 = np.linalg.norm(vetor, ord=1)
print(norma_l1)
Saída do Código
6.0
A norma L2 mede a distância do vetor até a origem, levando em conta o “comprimento reto” no espaço vetorial:
Aplicação prática:
Regularização L2 (weight decay) para evitar overfitting.
Cálculo de distância entre embeddings em tarefas como reconhecimento facial.
# Norma L2 (Euclidiana)
norma_l2 = np.linalg.norm(vetor) # padrão é a norma L2
print(norma_l2)
Saída do Código
3.7416573867739413
Nota: A função
np.linalg.normcalcula, por padrão, a norma L2. Para outras normas, como L1, é necessário especificar o parâmetroord.
Visualizando as Normas
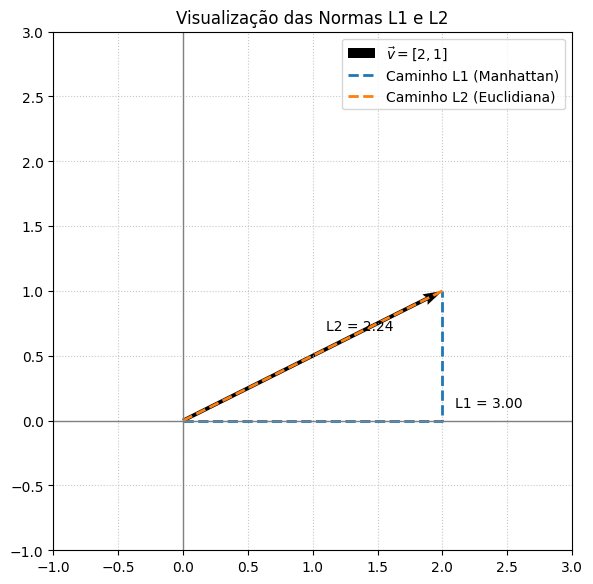
A seguir, temos uma representação gráfica das normas L1 e L2 para o vetor \(\vec{v} = [2, 1]\):
Linha sólida: representa o vetor original.
Linha tracejada para L1: caminho em forma de “escada”, que soma os deslocamentos absolutos nas direções x e y.
Linha tracejada para L2: caminho retilíneo direto da origem até o ponto, correspondente à distância euclidiana.
Essa visualização ajuda a entender a diferença conceitual entre as normas:
L1 mede deslocamentos em eixos ortogonais;
L2 mede a distância “em linha reta” até o destino.
import numpy as np
import matplotlib.pyplot as plt
# Vetor de exemplo
v = np.array([2, 1])
# Cálculo das normas
norma_l1 = np.linalg.norm(v, ord=1) # 3.0
norma_l2 = np.linalg.norm(v) # 2.23606797749979
# Plotagem
fig, ax = plt.subplots(figsize=(6, 6))
# Vetor
ax.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1,
linewidth=2, label=r'$\vec{v} = [2, 1]$')
# Caminhos
ax.plot([0, v[0], v[0]], [0, 0, v[1]], '--', linewidth=2, label='Caminho L1 (Manhattan)')
ax.plot([0, v[0]], [0, v[1]], '--', linewidth=2, label='Caminho L2 (Euclidiana)')
# Anotações
ax.text(2.1, 0.1, f'L1 = {norma_l1:.2f}', fontsize=10)
ax.text(1.1, 0.7, f'L2 = {norma_l2:.2f}', fontsize=10)
# Ajustes do gráfico
ax.set_xlim(-1, 3)
ax.set_ylim(-1, 3)
ax.set_aspect('equal')
ax.grid(True, linestyle=':', alpha=0.7)
ax.axhline(0, color='gray', lw=1)
ax.axvline(0, color='gray', lw=1)
ax.legend()
ax.set_title('Visualização das Normas L1 e L2', fontsize=12)
plt.tight_layout()
plt.show()
Cálculo em Machine Learning#
O cálculo é uma das ferramentas matemáticas fundamentais para o funcionamento de algoritmos de machine learning. Ele está diretamente relacionado com o processo de otimização, no qual ajustamos os parâmetros de um modelo para minimizar uma função de custo e, assim, melhorar o desempenho do modelo.
Derivadas Parciais (Gradientes)#
As derivadas parciais indicam como pequenas variações em um parâmetro específico afetam o valor de uma função. No contexto de ML, usamos derivadas parciais para calcular como cada parâmetro influencia o erro do modelo — isso é o que chamamos de gradiente.
Aplicação Prática:
Durante o treinamento de um modelo (como uma rede neural), utilizamos o gradiente da função de custo em relação aos pesos para saber como atualizá-los. Isso é feito com algoritmos como gradiente descendente.
Definição Matemática:
Se temos uma função \(f(x_1, x_2, \ldots, x_n)\), a derivada parcial em relação a \(x_i\) é:
Exemplo Analítico:
Considere \(f(x, y) = x^2 + 3y\).
Então:
\(\frac{\partial f}{\partial x} = 2x \Rightarrow \frac{\partial f}{\partial x}(2, 1) = 4\)
\(\frac{\partial f}{\partial y} = 3 \Rightarrow \frac{\partial f}{\partial y}(2, 1) = 3\)
Exemplo em Python:
def f(x, y):
return x**2 + 3*y
def derivada_parcial_x(f, x, y, delta=1e-5):
return (f(x + delta, y) - f(x, y)) / delta
def derivada_parcial_y(f, x, y, delta=1e-5):
return (f(x, y + delta) - f(x, y)) / delta
print("∂f/∂x:", derivada_parcial_x(f, 2, 1))
print("∂f/∂y:", derivada_parcial_y(f, 2, 1))
Saída:
∂f/∂x: 4.000009999951316
∂f/∂y: 3.000000248221113
Gradiente#
O gradiente de uma função multivariada é um vetor composto pelas derivadas parciais em relação a todos os seus parâmetros. Ele indica a direção de maior crescimento da função — ou seja, é usado para decidir para onde mover os pesos na minimização da função de custo.
Definição Matemática:
Se \(J(\theta)\) é a função de custo e \(\theta = [\theta_1, \theta_2, \ldots, \theta_n]\) os parâmetros do modelo:
Exemplo Analítico:
Considere \(J(\theta_1, \theta_2) = \theta_1^2 + \theta_2^2\).
Então:
\(\frac{\partial J}{\partial \theta_1} = 2\theta_1 \Rightarrow 2\)
\(\frac{\partial J}{\partial \theta_2} = 2\theta_2 \Rightarrow 4\)
Gradiente: \(\nabla J(\theta) = [2, 4]\) para \(\theta = [1, 2]\)
Exemplo em Python:
import numpy as np
def J(theta):
return theta[0]**2 + theta[1]**2
def gradiente(J, theta, delta=1e-5):
grad = np.zeros_like(theta)
for i in range(len(theta)):
theta_up = np.copy(theta)
theta_up[i] += delta
grad[i] = (J(theta_up) - J(theta)) / delta
return grad
theta = np.array([1.0, 2.0])
print("Gradiente:", gradiente(J, theta))
Saída:
Gradiente: [2.00000001 4.00000033]
Aqui está a versão revisada com a explicação didática sobre a regra da cadeia — com o foco na ideia intuitiva de “derivar por fora e depois por dentro”, mantendo toda a estrutura e formatação que você pediu:
Regra da Cadeia#
A regra da cadeia é uma técnica fundamental do cálculo usada para derivar funções compostas — isto é, quando uma função está “dentro” de outra. Em machine learning, essa regra é essencial durante o backpropagation (retropropagação do erro), pois as redes neurais profundas consistem em múltiplas camadas de funções encadeadas.
💡 Intuição didática:
Para derivar uma função composta, primeiro derivamos a função de fora (a mais externa), mantendo a de dentro intacta, e depois multiplicamos pela derivada da função de dentro.É como “descascar uma cebola”: você começa de fora para dentro.
Definição Matemática
Se temos duas funções:
\(u = g(x)\)
\(y = f(u)\)
Então a derivada de \(y\) com relação a \(x\) é:
Exemplo Analítico
Seja:
\(g(x) = 3x + 1\)
\(f(u) = u^2 \Rightarrow f(g(x)) = (3x + 1)^2\)
A derivada de \(f(g(x))\) usando a regra da cadeia será:
Calculando cada parte:
\(f'(u) = 2u \Rightarrow f'(g(x)) = 2(3x + 1)\)
\(g'(x) = 3\)
Logo:
Substituindo \(x = 2\):
Exemplo em Python
def f(u):
return u**2 # f(u) = u²
def g(x):
return 3*x + 1 # g(x) = 3x + 1
def composicao(x):
return f(g(x)) # f(g(x)) = (3x + 1)²
def derivada(x):
df_du = 2 * g(x) # f'(g(x)) = 2 * (3x + 1)
du_dx = 3 # g'(x) = 3
return df_du * du_dx # Regra da cadeia
# Teste no ponto x = 2
x = 2
print("Valor da função composta:", composicao(x)) # Deve ser 49
print("Derivada via regra da cadeia:", derivada(x)) # Deve ser 42
Saída esperada:
Valor da função composta: 49
Derivada via regra da cadeia: 42
Redes Neurais Artificiais (ANNs)#
As Redes Neurais Artificiais (ANNs) são modelos computacionais inspirados no funcionamento do cérebro humano. Elas conseguem aprender padrões complexos a partir de dados, sendo amplamente utilizadas em tarefas como reconhecimento de imagens, processamento de linguagem natural e previsão de séries temporais.
Neste material, exploraremos os principais conceitos de forma passo a passo: começando pelo neurônio artificial, passando pelo processo de aprendizado (ajuste de pesos, propagação e retropropagação), e finalizando com a otimização da rede.
O Neurônio Artificial: A Unidade Básica#
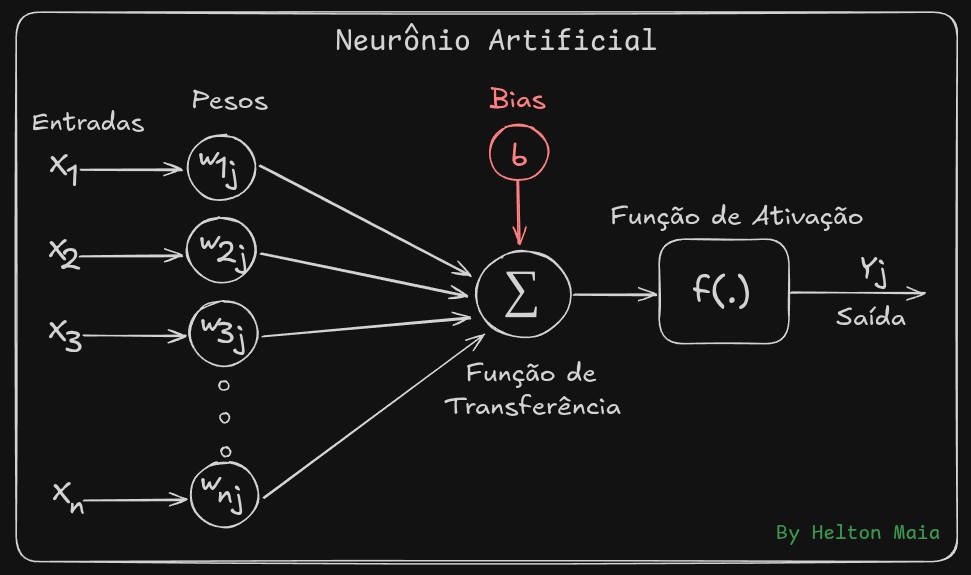
O neurônio artificial é o bloco fundamental de uma rede neural. Ele simula o comportamento de um neurônio biológico, processando informações da seguinte maneira:
Recebe entradas (\(x_1, x_2, \ldots, x_n\)).
Multiplica cada entrada por um peso (\(w_1, w_2, \ldots, w_n\)), que indica sua importância.
Soma todas as entradas ponderadas e adiciona um bias (\(b\)), um termo de ajuste que auxilia no aprendizado.
Passa o resultado por uma função de ativação (\(f\)), que decide se o neurônio deve ser ativado.
Expressão matemática de um neurônio:
Onde:
\(x_i\): Valores de entrada.
\(w_i\): Pesos (ajustáveis durante o treinamento).
\(b\): Bias (ajusta o limiar de ativação).
\(f\): Função de ativação (introduz não-linearidade).
\(y\): Saída do neurônio.
Visualização de um Neurônio Artificial#
Pesos e Bias: Como a Rede Aprende?#
Os pesos (\(w_i\)) e o bias (\(b\)) são os parâmetros ajustáveis que determinam o comportamento da rede neural durante o aprendizado.
Pesos (\(w_i\)) determinam a influência de cada entrada na saída:
Se \(w_i\) é grande, a entrada tem maior impacto.
Se \(w_i\) é pequeno ou próximo de zero, a entrada é quase ignorada.
Bias (\(b\)) define o limiar de ativação, permitindo que o neurônio ative mesmo com uma soma ponderada baixa.
Como os pesos são ajustados?
Inicialização aleatória.
A rede compara a saída gerada com a resposta esperada (cálculo do erro).
Utilizando gradiente descendente, os pesos e o bias são ajustados para minimizar o erro.
Propagação (Forward Propagation)#
A propagação direta (forward propagation) é o processo em que os dados de entrada passam pela rede, camada por camada, até gerar uma saída.
Etapas principais:
Entrada → Camadas Ocultas:
Cada neurônio calcula a ativação com base na soma ponderada + bias.
A função de ativação é aplicada.
Camadas Ocultas → Saída:
O processo se repete até a última camada.
A saída final é usada para calcular o erro comparando-a com a saída esperada.
Cálculo do Erro: Medindo o Desempenho#
O erro, também chamado de função de perda, mede quão longe a saída da rede está do valor real.
Funções de perda comuns:
Erro Quadrático Médio (MSE):
\[ L = \frac{1}{N} \sum_{i=1}^{N} (y_{\text{predito}} - y_{\text{real}})^2 \]Utilizada em problemas de regressão.
Entropia Cruzada (Cross-Entropy):
\[ L = -\sum_{i=1}^{N} y_{\text{real}} \log(y_{\text{predito}}) \]Utilizada em problemas de classificação.
Objetivo: Minimizar o erro ajustando os pesos e o bias da rede.
Funções de Ativação: Introduzindo Não-Linearidade#
Sem funções de ativação, uma rede neural seria apenas uma combinação linear de entradas, incapaz de aprender padrões complexos. As funções de ativação introduzem não-linearidade, permitindo que a rede modele relações mais sofisticadas.
Vamos começar, analisando um exemplo de Rede Sem Funções de Ativação.
Considere uma rede neural totalmente conectada com duas camadas lineares e sem função de ativação. Sua estrutura é a seguinte:
Arquitetura da Rede:
Entrada: vetor \(\mathbf{x} \in \mathbb{R}^2\), com duas características:
Primeira camada (oculta):
Pesos \(\mathbf{W}^{(1)} \in \mathbb{R}^{2 \times 2}\)
Bias \(\mathbf{b}^{(1)} \in \mathbb{R}^2\)
Segunda camada (saída):
Pesos \(\mathbf{W}^{(2)} \in \mathbb{R}^{1 \times 2}\)
Bias \(b^{(2)} \in \mathbb{R}\)
Etapas do Cálculo
Camada Oculta (linear, sem ativação):
Camada de Saída (também linear):
Resultado Final:
A saída da rede é \(y = 28\), que é linearmente dependente da entrada \(\mathbf{x}\), reforçando que sem funções de ativação, a composição de múltiplas camadas lineares ainda resulta em uma função linear.
Código Python
import numpy as np
# Entrada
x = np.array([[1], [2]]) # vetor coluna
# Parâmetros da primeira camada
W1 = np.array([[2, -1],
[0, 3]])
b1 = np.array([[1],
[-2]])
# Parâmetros da segunda camada (atualizados)
W2 = np.array([[3, 5]])
b2 = 5
# Forward pass sem ativação
h = W1 @ x + b1 # Saída da primeira camada
y = W2 @ h + b2 # Saída final
print(f"Saída da camada oculta h:\n{h}")
print(f"Saída final y: {y.item()}")
Saída esperada:
Saída da camada oculta h:
[[1]
[4]]
Saída final y: 28
Agora, vamos introduzir a Não-Linearidade de um reunônio ou rede neural artificial. Primeiramente, vamos conhecer algumas das principais funções de ativação. Veja a tabela a seguir:
Principais Funções de Ativação#
Função |
Fórmula |
Comportamento |
Aplicação |
|---|---|---|---|
Sigmoid |
\(\sigma(x) = \frac{1}{1 + e^{-x}}\) |
Mapeia qualquer valor para \((0, 1)\). Pode sofrer com vanishing gradient. |
Saída de classificadores binários. |
ReLU |
\(\text{ReLU}(x) = \max(0, x)\) |
Retorna \(x\) se positivo, senão \(0\). Simples e eficiente, mas pode zerar neurônios. |
Camadas ocultas em redes profundas. |
Tanh |
\(\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\) |
Mapeia para \((-1, 1)\). Saída centrada, mas ainda sofre com vanishing gradient. |
Camadas ocultas com dados normalizados. |
Leaky ReLU |
\(\text{LeakyReLU}(x) = \max(\alpha x, x),\ \alpha \approx 0.01\) |
Variante do ReLU que permite pequeno gradiente quando \(x < 0\). |
Evita o “neurônio morto” do ReLU. |
Softmax |
\(\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}\) |
Transforma vetor em uma distribuição de probabilidade. |
Saída de classificadores multiclasse. |
Visualização das Funções de Ativação e suas Derivadas
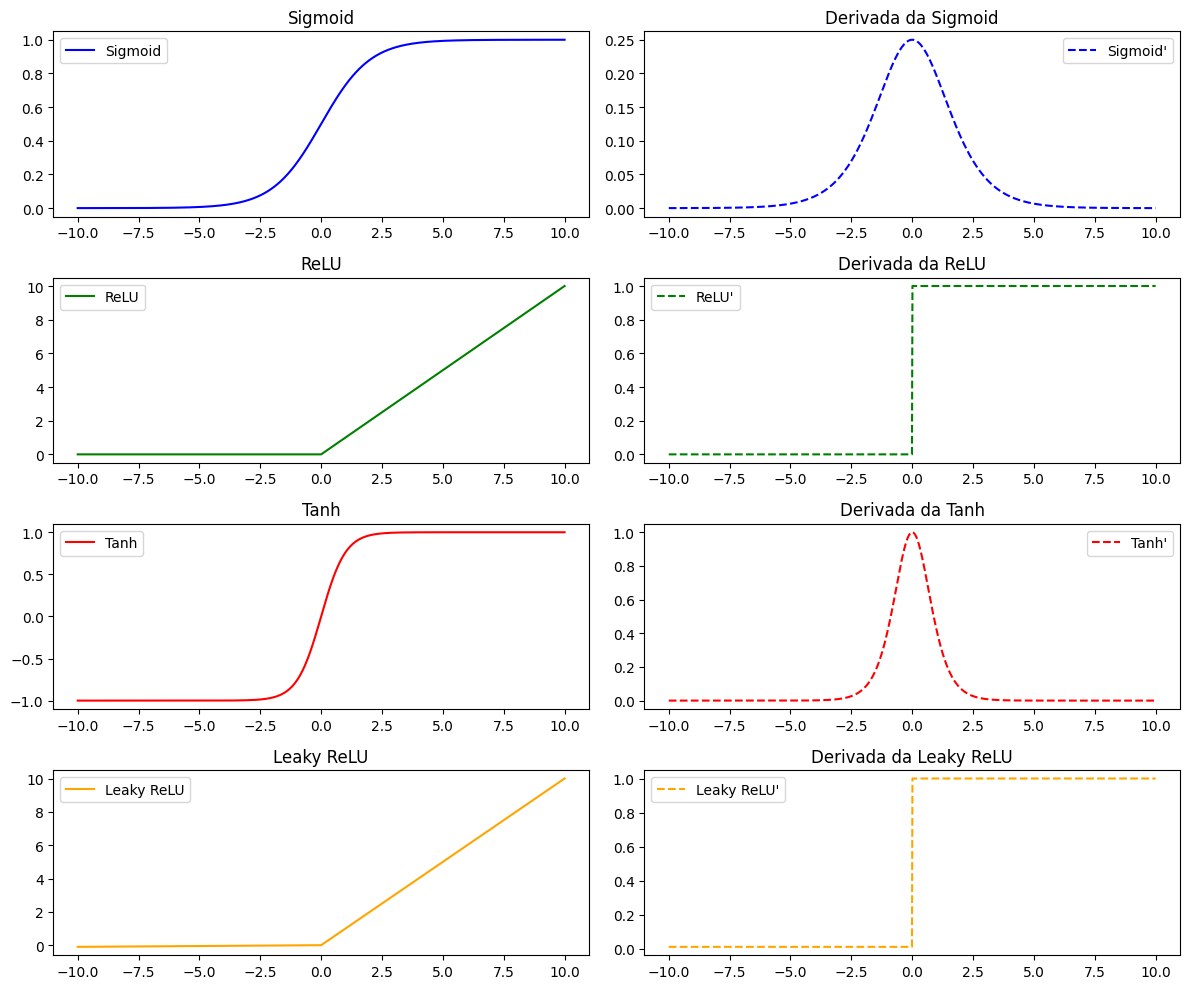
Incorporando a Função de Ativação#
A figura abaixo mostra visualmente, funções de ativação sendo incorporadas em nossa pequena rede artificial:
Ao aplicar, por exemplo, a função de ativação sigmoide após as multiplicações lineares, o modelo agora é capaz de capturar relações não-lineares entre as variáveis de entrada e a saída. A nova estrutura da rede se mantém idêntica, mas com ativação sigmoide aplicada tanto à saída da camada oculta quanto à saída final da rede:
A função sigmoide é definida por:
Etapas do Cálculo (com ativação sigmoide)
Camada Oculta (linear + ativação sigmoide)
Camada de Saída (linear + ativação sigmoide)
Resultado Final
Com a não-linearidade introduzida pela sigmoide em todas as camadas, a rede retorna:
O resultado agora não é mais uma combinação linear direta da entrada, o que mostra o poder da não-linearidade em redes neurais.
Código Python (com sigmoide na saída também)
import numpy as np
# Função sigmoide
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# Entrada
x = np.array([[1], [2]])
# Parâmetros da primeira camada
W1 = np.array([[2, -1],
[0, 3]])
b1 = np.array([[1],
[-2]])
# Parâmetros da segunda camada
W2 = np.array([[3, 5]])
b2 = 5
# Forward pass com ativação sigmoide em ambas as camadas
h_linear = W1 @ x + b1
h = sigmoid(h_linear)
z = W2 @ h + b2
y = sigmoid(z)
print(f"Saída linear da camada oculta (antes da ativação):\n{h_linear}")
print(f"Saída da camada oculta (após sigmoide):\n{h}")
print(f"Valor z (entrada da saída): {z.item():.3f}")
print(f"Saída final y (após sigmoide): {y.item():.6f}")
Saída esperada:
Saída linear da camada oculta (antes da ativação):
[[1]
[4]]
Saída da camada oculta (após sigmoide):
[[0.73105858]
[0.98201379]]
Valor z (entrada da saída): 12.103
Saída final y (após sigmoide): 0.999995
Calculando o Erro#
Após obter a saída da rede, podemos avaliar seu desempenho comparando-a com o valor real esperado. Essa comparação é feita por meio de uma função de perda, que mede a diferença entre a saída predita e a saída desejada. Uma das funções mais utilizadas para problemas de regressão é o Erro Quadrático Médio (MSE), definido como:
Onde:
\(L\) é o valor da perda (erro médio);
\(N\) é o número de amostras;
\(y_{\text{predito}}^{(i)}\) é a saída da rede para a \(i\)-ésima amostra;
\(y_{\text{real}}^{(i)}\) é o valor real esperado para a mesma amostra.
Exemplo prático (com N = 1):
Suponha que o valor real esperado seja:
E a saída da rede (com ativação sigmoide) seja:
Aplicando na fórmula do MSE:
Portanto, o erro quadrático médio é aproximadamente 0,249995, o que indica uma diferença relevante entre a predição da rede e o valor esperado.
Código Python (cálculo do erro MSE)
# Valor real esperado
y_real = 0.5
# Saída predita pela rede
y_predito = y.item()
# Cálculo do erro quadrático médio
mse = (y_predito - y_real) ** 2
print(f"Erro Quadrático Médio (MSE): {mse:.6f}")
Saída esperada:
Erro Quadrático Médio (MSE): 0.249995
🧠 Exercício: Simulação Interativa de uma Rede Neural Simples#
Neste exercício, você irá simular uma pequena rede neural composta por:
2 entradas
1 camada oculta com 2 neurônios
1 neurônio na saída
A saída será calculada em duas etapas:
Camada oculta (com ativação):
\[ \mathbf{h} = f(\mathbf{W}^{(1)} \cdot \mathbf{x} + \mathbf{b}^{(1)}) \]Camada de saída (com ativação):
\[ y = f(\mathbf{W}^{(2)} \cdot \mathbf{h} + b^{(2)}) \]
O que você deve implementar (com Gradio):
Crie uma interface interativa que permita:
Inserir manualmente ou gerar aleatoriamente os seguintes valores:
Vetor de entrada \(\mathbf{x} = [x_1, x_2]\)
Matriz de pesos da primeira camada \(\mathbf{W}^{(1)}\) (2×2)
Bias da primeira camada \(\mathbf{b}^{(1)}\) (2×1)
Vetor de pesos da segunda camada \(\mathbf{W}^{(2)}\) (1×2)
Bias da segunda camada \(b^{(2)}\)
Escolher a função de ativação:
Sigmoid
ReLU
Tanh
Leaky ReLU
Inserir o valor desejado (target):
Valor escalar \(y_{\text{true}}\) que representa a saída esperada do modelo.
Exibir os resultados do forward pass:
Saída da camada oculta \(\mathbf{h}\)
Valor intermediário \(z\) da saída
Saída final \(y = f(z)\)
Erro quadrático:
\[ \text{Erro} = (y - y_{\text{true}})^2 \]
Objetivo:
Explorar o comportamento de uma rede neural simples, observando como diferentes pesos, vieses e funções de ativação afetam o resultado da predição — e comparando com o valor esperado (target) para analisar o erro da rede.
Sugestão Visual: Após clicar em “Calcular”, é desejado que seja gerada automaticamente uma figura representando:
Os neurônios (entradas, camada oculta e saída),
As conexões entre eles,
Os pesos associados a cada conexão,
As ativações intermediárias e finais,
E os valores numéricos em cada etapa.
Isso facilita a compreensão do fluxo de dados na rede e torna o comportamento da rede mais intuitivo para o usuário.
💡 Dica técnica: bibliotecas como
graphviz,networkxoumatplotlibpodem ser utilizadas para gerar essa visualização de forma programática.
Backpropagation (Começando pela Camada de Saída)#
Para que uma rede neural aprenda, ela precisa ajustar seus pesos e biases de forma a reduzir o erro entre a saída predita e o valor real. Esse ajuste é feito por meio do algoritmo de retropropagação do erro (backpropagation), que calcula o gradiente da função de perda em relação aos parâmetros da rede.
Visão Geral da Retropropagação
A lógica da retropropagação segue a regra da cadeia da derivada: partimos do erro final da rede e voltamos etapa por etapa até os parâmetros, aplicando:
∂L/∂W = ∂L/∂y · ∂y/∂z · ∂z/∂W
Neste caso:
L é a função de perda;
y é a saída da rede;
z é a entrada da função de ativação na última camada;
W representa os pesos da camada de saída.
Funções utilizadas
Função de perda (Erro Quadrático Médio - MSE):
\[ L = \frac{1}{2}(y - y_{\text{real}})^2 \]O fator $\frac{1}{2}$ é utilizado para simplificar a derivada.
Função de ativação (Sigmoide):
\[ \sigma(z) = \frac{1}{1 + e^{-z}}, \quad \sigma'(z) = \sigma(z)(1 - \sigma(z)) \]
Etapas da Retropropagação#
1. Derivada da perda em relação à saída da rede
A saída da rede é \(y\) e o valor esperado é \(y_{\text{real}}\):
2. Derivada da saída em relação à entrada da função de ativação
Sabemos que:
Logo, aplicando a derivada da função sigmoide:
3. Derivada da perda em relação a \(z\) (entrada da camada de saída)
Aplicando a regra da cadeia:
Esse valor representa o erro propagado na saída e é comumente chamado de:
Gradientes para Ajuste de Parâmetros#
Por que usamos \(\delta \cdot \mathbf{h}^T\) para calcular \(\partial L / \partial \mathbf{W}^{(2)}\)?
A entrada \(z\) depende dos pesos da forma:
Portanto:
Para o bias:
Como \(z\) depende linearmente do bias com derivada igual a 1:
Cálculo Numérico
Com:
Temos:
Código: Gradientes da Saída
# Derivada da sigmoide
def sigmoid_deriv(z):
s = sigmoid(z)
return s * (1 - s)
# y_real já definido
y_real = 0.5
# Derivadas
dL_dy = y - y_real # ∂L/∂y
dy_dz = sigmoid_deriv(z) # ∂y/∂z
dL_dz = dL_dy * dy_dz # ∂L/∂z
# Gradientes para W2 e b2
dL_dW2 = dL_dz * h.T
dL_db2 = dL_dz
print(f"∂L/∂z (delta): {dL_dz.item():.8f}")
print(f"Gradiente de W2: {dL_dW2}")
print(f"Gradiente de b2: {dL_db2.item():.8f}")
Saída esperada:
∂L/∂z (delta): 0.00000250
Gradiente de W2: [[1.8275e-06 2.4550e-06]]
Gradiente de b2: 0.00000250
Backpropagation na Camada Oculta#
Agora que já calculamos o erro da camada de saída, vamos entender como esse erro se propaga para a primeira camada, afetando os pesos $\mathbf{W}^{(1)}$e os bias $\mathbf{b}^{(1)}$.
Usamos os seguintes valores:
Entrada: \(\mathbf{x} = \begin{bmatrix} 1 \ 2 \end{bmatrix} \)
Pesos da 1ª camada: \(\mathbf{W}^{(1)} = \begin{bmatrix} 2 & -1 \ 0 & 3 \end{bmatrix} \)
Bias da 1ª camada: \(\mathbf{b}^{(1)} = \begin{bmatrix} 1 \ -2 \end{bmatrix} \)
Saída linear da camada oculta: \(\mathbf{h}\_{\text{linear}} = \begin{bmatrix} 1 \ 4 \end{bmatrix} \)
Saída com ativação (sigmoide): \(\mathbf{h} \approx \begin{bmatrix} 0{,}731 \ 0{,}982 \end{bmatrix} \)
1. Derivada da perda em relação à saída da camada oculta \(\mathbf{h} \)
A saída da rede é:
Aplicando a regra da cadeia:
Com:
\(\delta = \frac{\partial L}{\partial z} \approx 2{,}5 \times 10^{-6} \)
\(\mathbf{W}^{(2)} = [3 \quad 5] \)
Obtemos:
2. Derivada da função sigmoide na camada oculta
Calculando:
Para \(z = 1 \): \(\sigma(1) \approx 0{,}731 \Rightarrow \sigma'(1) \approx 0{,}197 \)
Para \(z = 4 \): \(\sigma(4) \approx 0{,}982 \Rightarrow \sigma'(4) \approx 0{,}018 \)
Então:
3. Derivada da perda em relação à entrada da sigmoide
Aplicamos o produto elemento a elemento:
4. Gradiente da perda em relação aos pesos da 1ª camada \(\mathbf{W}^{(1)} \)
A derivada é dada por:
Com:
\(\delta\_{\text{oculta}} = \frac{\partial L}{\partial \mathbf{h}\_{\text{linear}}} \)
\(\mathbf{x}^T = \begin{bmatrix} 1 & 2 \end{bmatrix} \)
Este é um produto vetor coluna × vetor linha, resultando numa matriz:
5. Gradiente da perda em relação ao bias da 1ª camada
O bias é somado diretamente, então:
Resumo da cadeia de derivadas para \(\mathbf{W}^{(1)} \):
Código: Gradientes da Camada Oculta
# Derivadas da sigmoide
h_deriv = sigmoid_deriv(h_linear)
# Gradiente da perda em relação à saída da camada oculta
dL_dh = delta @ W2 # delta é (1,1), W2 é (1,2) → resultado (1,2)
# Derivada em relação à entrada da sigmoide
dL_dh_linear = dL_dh.T * h_deriv # Transpõe dL_dh e faz produto elemento a elemento
# Gradiente de W1 e b1
dL_dW1 = dL_dh_linear @ x.T
dL_db1 = dL_dh_linear
print(f"Gradiente de W1:\n{dL_dW1}")
print(f"Gradiente de b1:\n{dL_db1}")
Saída Esperada
Gradiente de W1:
[[1.4801e-06 2.9602e-06]
[2.2499e-07 4.4999e-07]]
Gradiente de b1:
[[1.4801e-06]
[2.2499e-07]]
Esses valores agora podem ser utilizados na atualização dos pesos com gradiente descendente:
# Atualização dos parâmetros da primeira camada
W1 -= eta * dL_dW1
b1 -= eta * dL_db1
Esses gradientes nos dizem como cada peso e bias da camada oculta contribuem para o erro total. Ao subtrairmos uma fração proporcional a eles (usando a taxa de aprendizado $\eta $), ajustamos os parâmetros para reduzir o erro da rede.
Resumo Completo: Ciclo de Treinamento#
Usamos:
Entrada \(\mathbf{x} = \begin{bmatrix} 1 \ 2 \end{bmatrix}\)
Função de ativação: sigmoide
Função de perda: Erro Quadrático Médio (MSE)
Valor real esperado: \(y\_{\text{real}} = 0{,}5\)
Forward Pass
Camada oculta (linear + sigmoide):
\[\begin{split} \mathbf{h}_{\text{linear}} = \mathbf{W}^{(1)} \mathbf{x} + \mathbf{b}^{(1)} = \begin{bmatrix} 0{,}1 \\ 0{,}4 \end{bmatrix} \Rightarrow \mathbf{h} = \sigma(\mathbf{h}_{\text{linear}}) \approx \begin{bmatrix} 0{,}525 \\ 0{,}598 \end{bmatrix} \end{split}\]Camada de saída (linear + sigmoide):
\[ z = \mathbf{W}^{(2)} \cdot \mathbf{h} + b^{(2)} = 0{,}990 \Rightarrow y = \sigma(z) \approx 0{,}7291 \]
Cálculo da perda
Erro real esperado: \(y\_{\text{real}} = 0{,}5\)
Backpropagation
Gradiente da saída:
\[ \delta_{\text{output}} = (y - y_{\text{real}}) \cdot \sigma'(z) \approx 0{,}2291 \cdot (1 - 0{,}7291) \cdot 0{,}7291 \approx 0{,}0450 \]Gradientes da segunda camada:
\[ \frac{\partial L}{\partial \mathbf{W}^{(2)}} = \delta \cdot \mathbf{h}^T \approx \begin{bmatrix} 0{,}0237 & 0{,}0270 \end{bmatrix} \quad,\quad \frac{\partial L}{\partial b^{(2)}} = \delta = 0{,}0450 \]Gradientes da primeira camada:
\[\begin{split} \frac{\partial L}{\partial \mathbf{W}^{(1)}} \approx \begin{bmatrix} 0{,}000685 & 0{,}001371 \\ 0{,}000909 & 0{,}001818 \end{bmatrix} \quad,\quad \frac{\partial L}{\partial \mathbf{b}^{(1)}} \approx \begin{bmatrix} 0{,}000685 \\ 0{,}000909 \end{bmatrix} \end{split}\]
Atualização dos Pesos
Usando taxa de aprendizado \(\eta = 0{,}005\):
Código Final Completo
import numpy as np
# Funções
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def sigmoid_deriv(z):
s = sigmoid(z)
return s * (1 - s)
# Dados
x = np.array([[1], [2]])
y_real = 0.5
eta = 0.005
# Inicialização
W1 = np.array([[0.2, -0.1],
[0.0, 0.3]])
b1 = np.array([[0.1],
[-0.2]])
W2 = np.array([[0.3, 0.5]])
b2 = np.array([[0.5]])
# Forward Pass
h_linear = W1 @ x + b1
h = sigmoid(h_linear)
z = W2 @ h + b2
y_pred = sigmoid(z)
# Loss
mse = (y_pred.item() - y_real)**2
# Gradiente da saída
dy_dz = sigmoid_deriv(z)
delta = (y_pred - y_real) * dy_dz
# Gradientes da segunda camada
dL_dW2 = delta @ h.T
dL_db2 = delta
# Gradientes da primeira camada
dL_dh = W2.T @ delta
dh_dh_linear = sigmoid_deriv(h_linear)
dL_dh_linear = dL_dh * dh_dh_linear
dL_dW1 = dL_dh_linear @ x.T
dL_db1 = dL_dh_linear
# Atualização dos parâmetros
W2 -= eta * dL_dW2
b2 -= eta * dL_db2
W1 -= eta * dL_dW1
b1 -= eta * dL_db1
# Novo Forward Pass
h_linear_new = W1 @ x + b1
h_new = sigmoid(h_linear_new)
z_new = W2 @ h_new + b2
y_new = sigmoid(z_new)
print(f"Saída original da rede: {y_pred.item():.6f}")
print(f"Erro MSE: {mse:.6f}")
print(f"Saída após atualização: {y_new.item():.6f}")
Resultado Final
A saída esperada será algo como:
Saída original da rede: 0.729103
Erro MSE: 0.052469
Saída após atualização: 0.728558
Ou seja, houve uma pequena correção na direção do valor real desejado (0.5). Esse processo pode ser repetido em ciclos sucessivos até que a rede aprenda a produzir saídas cada vez mais próximas do valor alvo.
Treinamento Funcional#
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def sigmoid_deriv(z):
s = sigmoid(z)
return s * (1 - s)
# Dados de entrada
x = np.array([[1], [2]])
y_real = 0.5
# Hiperparâmetros
eta = 0.005 # Taxa de aprendizado ajustada
epochs = 10000
# Inicialização dos pesos com valores menores para evitar saturação
W1 = np.array([[0.2, -0.1],
[0.0, 0.3]])
b1 = np.array([[0.1],
[-0.2]])
W2 = np.array([[0.3, 0.5]])
b2 = np.array([[0.5]])
# Loop de treinamento
for epoch in range(1, epochs+1):
# FORWARD PASS
h_linear = W1 @ x + b1
h = sigmoid(h_linear)
z = W2 @ h + b2
y_pred = sigmoid(z)
# Cálculo da perda
mse = (y_pred.item() - y_real)**2
# BACKPROPAGATION
dy_dz = sigmoid_deriv(z)
delta = (y_pred - y_real) * dy_dz
# Gradientes da camada de saída
dL_dW2 = delta @ h.T
dL_db2 = delta
# Gradientes da camada oculta
dL_dh = W2.T @ delta
dh_dh_linear = sigmoid_deriv(h_linear)
dL_dh_linear = dL_dh * dh_dh_linear
dL_dW1 = dL_dh_linear @ x.T
dL_db1 = dL_dh_linear
# Atualização dos pesos
W2 -= eta * dL_dW2
b2 -= eta * dL_db2
W1 -= eta * dL_dW1
b1 -= eta * dL_db1
if epoch % 1000 == 0 or epoch == 1:
print(f"Época {epoch:5d} | y_pred = {y_pred.item():.6f} | MSE = {mse:.6f}")
print("\nPesos finais:")
print("W1 =\n", W1)
print("b1 =\n", b1)
print("W2 =\n", W2)
print("b2 =\n", b2)
Saída esperada (resumida)
Época 1 | y_pred = 0.710949 | MSE = 0.044290
Época 1000 | y_pred = 0.536874 | MSE = 0.001358
Época 5000 | y_pred = 0.502849 | MSE = 0.000008
Época 10000 | y_pred = 0.500973 | MSE = 0.000001
A saída da rede, y_pred, converge suavemente para o valor esperado 0.5 e o erro quadrático médio (MSE) reduz consistentemente — isso confirma que o treinamento está correto e efetivo.
1 Neurônio#
Forward e Backpropagation#
Vamos para um caso simples para facilitar o entendimento. Depois, você pode voltar e rever o item para uma pequena rede.
Este exemplo demonstra o treinamento de um único neurônio com dois inputs. A ideia é mostrar, passo a passo, como o algoritmo de backpropagation atualiza os pesos para minimizar o erro entre a saída prevista e a saída real.
Dados de entrada e saída
Entradas:
x = [0.6, 0.3]Saída real (esperada):
y_real = 0.8Pesos iniciais:
w = [0.4, -0.1]Bias inicial:
b = 0.2Taxa de aprendizado:
α = 0.1
Forward Pass
Cálculo da soma ponderada \(z\):
Ativação (função sigmoide):
Função de perda (erro quadrático médio):
Backpropagation – Passo a Passo com Expressões e Cálculos
1. Derivada da função de perda:
2. Derivada da sigmoide:
3. Derivada da perda em relação a \(z\):
4. Derivadas da perda em relação aos pesos e bias:
5. Atualização dos parâmetros:
Quadro Resumo das Expressões Matemáticas
Passo |
Expressão |
|---|---|
Forward Pass |
|
Soma Ponderada (\(z\)) |
\(z = x_1 w_1 + x_2 w_2 + b\) |
Ativação (\(\sigma(z)\)) |
\(\sigma(z) = \frac{1}{1 + e^{-z}}\) |
Função de Perda |
\(\text{Loss} = (y_{\text{pred}} - y_{\text{real}})^2\) |
Backpropagation |
|
Derivada da Perda |
\(\frac{\partial L}{\partial y_{\text{pred}}} = 2(y_{\text{pred}} - y_{\text{real}})\) |
Derivada da Sigmoide |
\(\frac{\partial y_{\text{pred}}}{\partial z} = y_{\text{pred}}(1 - y_{\text{pred}})\) |
Derivada da Perda em relação a \(z\) |
\(\frac{\partial L}{\partial z} = \frac{\partial L}{\partial y_{\text{pred}}} \cdot \frac{\partial y_{\text{pred}}}{\partial z}\) |
Derivada da Perda em relação a \(w_1\) |
\(\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial z} \cdot x_1\) |
Derivada da Perda em relação a \(w_2\) |
\(\frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial z} \cdot x_2\) |
Derivada da Perda em relação a \(b\) |
\(\frac{\partial L}{\partial b} = \frac{\partial L}{\partial z}\) |
Atualização de \(w_1\) |
\(w_1 = w_1 - \alpha \cdot \frac{\partial L}{\partial w_1}\) |
Atualização de \(w_2\) |
\(w_2 = w_2 - \alpha \cdot \frac{\partial L}{\partial w_2}\) |
Atualização de \(b\) |
\(b = b - \alpha \cdot \frac{\partial L}{\partial b}\) |
Código Final – Uma Época
import numpy as np
# Entrada e saída desejada
x = np.array([0.6, 0.3])
y_real = 0.8
# Pesos e bias iniciais
w = np.array([0.4, -0.1])
b = 0.2
alpha = 0.1 # taxa de aprendizado
# Função sigmoide
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# Forward
z = np.dot(x, w) + b
y_pred = sigmoid(z)
loss = (y_pred - y_real)**2
print(f"Forward:")
print(f" z = {z:.4f}")
print(f" y_pred = {y_pred:.4f}")
print(f" loss = {loss:.4f}")
# Backpropagation
dL_dypred = 2 * (y_pred - y_real)
dypred_dz = y_pred * (1 - y_pred)
dL_dz = dL_dypred * dypred_dz
dL_dw = dL_dz * x
dL_db = dL_dz
# Atualização dos pesos e bias
w = w - alpha * dL_dw
b = b - alpha * dL_db
print("\nBackpropagation:")
print(f" dL_dypred = {dL_dypred:.4f}")
print(f" dypred_dz = {dypred_dz:.4f}")
print(f" dL_dz = {dL_dz:.4f}")
print(f" dL_dw = {dL_dw}")
print(f" dL_db = {dL_db:.4f}")
print("\nPesos e bias atualizados:")
print(f" w = {w}")
print(f" b = {b:.4f}")
# Nova predição após uma época
z = np.dot(x, w) + b
y_pred = sigmoid(z)
print(f"\nNova predição: {y_pred:.4f}")
Exercício: Treinamento de um Neurônio com Múltiplas Épocas#
Objetivo:
Modificar o código existente para treinar um neurônio com 1000 épocas, armazenando e plotando o erro e a acurácia ao longo do treinamento.
Tarefas:
Implemente o loop de treinamento:
Calcule
y_pred, o erro (MSE) e atualize os pesos (w,b) via backpropagation em cada época.Salve o erro e a acurácia em listas.
Plote os resultados:
Gráfico do erro (azul) e acurácia (laranja) por época.
Inclua legendas, título e labels (
Época,Erro/Acurácia).
Dica: Use matplotlib ou outra biblioteca para visualização e modelagem do neurônio graficamente.
Exemplo de saída:
Época 0: Erro = 0.0236 | Acurácia = 0.9764
Época 10: Erro = 0.0021 | Acurácia = 0.9979
...
Regressão Linear com um Único Neurônio usando o Keras#
A regressão linear é uma técnica estatística fundamental usada para modelar a relação entre uma variável de entrada $x$ (independente) e uma variável de saída $y$ (dependente), assumindo que essa relação é linear. O modelo busca ajustar a melhor reta que aproxima os dados, representada pela equação:
onde:
\(y\) é o valor previsto,
\(x\) é a variável de entrada,
\(w\) é o peso, também chamado de coeficiente angular ou inclinação da reta,
\(b\) é o viés (bias), ou intercepto da reta com o eixo \(y\).
Essa equação é exatamente o que um neurônio realiza quando usamos uma camada densa com uma unidade e sem função de ativação. Isso torna possível implementar a regressão linear com apenas um neurônio!
Geração dos Dados
import numpy as np
import matplotlib.pyplot as plt
# Gerar dados com ruído (reta com leve aleatoriedade)
np.random.seed(42)
x = np.linspace(0, 10, 100)
noise = np.random.normal(0, 1, size=x.shape)
y = 2 * x + 1 + noise * 2 # Reta base: y = 2x + 1 com ruído
Modelo com Keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD
from tensorflow.keras import Input
from sklearn.metrics import mean_squared_error
# Criar modelo com um único neurônio (sem função de ativação)
model = Sequential([
Input(shape=(1,)),
Dense(units=1)
])
model.compile(optimizer=SGD(learning_rate=0.001), loss='mse')
# Predições antes do treino
y_pred_initial = model.predict(x).flatten()
mse_before = mean_squared_error(y, y_pred_initial)
# Treinamento
history = model.fit(x, y, epochs=20, verbose=1)
# Predições depois do treino
y_pred = model.predict(x).flatten()
mse_after = mean_squared_error(y, y_pred)
Resultados e Visualizações
Comparação Antes e Depois do Treinamento:
# Subplots: antes e depois do treino
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# Gráfico 1: Antes do Treinamento — Dados, Reta Verdadeira e Reta Inicial
axs[0].scatter(x, y, color='blue', label='Dados com ruído')
axs[0].plot(x, 2 * x + 1, 'r--', label='Reta verdadeira: y=2x+1')
axs[0].plot(x, y_pred_initial, 'gray', label='Reta inicial')
axs[0].set_title(f'Antes do Treinamento\nMSE = {mse_before:.2f}')
axs[0].set_xlabel('x')
axs[0].set_ylabel('y')
axs[0].legend()
axs[0].grid(True)
# Gráfico 2: Depois do Treinamento — Dados, Reta Verdadeira e Reta Aprendida
axs[1].scatter(x, y, color='blue', label='Dados com ruído')
axs[1].plot(x, 2 * x + 1, 'r--', label='Reta verdadeira')
axs[1].plot(x, y_pred, 'g-', label='Reta aprendida')
axs[1].set_title(f'Depois do Treinamento\nMSE = {mse_after:.2f}')
axs[1].set_xlabel('x')
axs[1].set_ylabel('y')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
Evolução do Erro e Acurácia Adaptada:
# Calcular acurácia adaptada como 1 - erro normalizado
loss = np.array(history.history['loss'])
acc = 1 - loss / np.max(loss)
# Plotar erro e acurácia
fig, axs = plt.subplots(1, 2, figsize=(14, 4))
axs[0].plot(loss, label='Erro (MSE)', color='red')
axs[0].set_title('Erro durante o Treinamento')
axs[0].set_xlabel('Épocas')
axs[0].set_ylabel('MSE')
axs[0].grid(True)
axs[0].legend()
axs[1].plot(acc, label='Acurácia adaptada', color='green')
axs[1].set_title('Acurácia (1 - erro normalizado)')
axs[1].set_xlabel('Épocas')
axs[1].set_ylabel('Acurácia')
axs[1].grid(True)
axs[1].legend()
plt.tight_layout()
plt.show()
Parâmetros Aprendidos
# Extrair os pesos aprendidos (w e b)
w, b = model.layers[0].get_weights()
print(f'Parâmetros aprendidos:')
print(f' Inclinação (w): {w[0][0]:.4f}')
print(f' Intercepto (b): {b[0]:.4f}')
Parâmetros aprendidos:
Inclinação (w): 1.9876
Intercepto (b): 1.0342
Esses valores mostram que o neurônio conseguiu aprender uma reta muito próxima da verdadeira \(y = 2x + 1\), mesmo com ruído nos dados — o que é uma ótima ilustração de como redes neurais podem resolver problemas simples de regressão linear.
Plote com os valores extraídos:
# Usar os pesos aprendidos para calcular a reta
w_val = w[0][0]
b_val = b[0]
reta_aprendida = w_val * x + b_val
# Plotar os dados e a reta aprendida manualmente
plt.figure(figsize=(8, 5))
plt.scatter(x, y, color='blue', label='Dados com ruído')
plt.plot(x, 2 * x + 1, 'r--', label='Reta verdadeira: y=2x+1')
plt.plot(x, reta_aprendida, 'g-', label=f'Reta aprendida: y={w_val:.2f}x+{b_val:.2f}')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Visualização da Reta Aprendida')
plt.legend()
plt.grid(True)
plt.show()
Redes Neurais com Múltiplas Camadas#
As redes neurais artificiais (RNAs), inspiradas no funcionamento do cérebro humano, são ferramentas poderosas no campo do aprendizado de máquina. Vamos explorar sua estrutura e funcionamento:
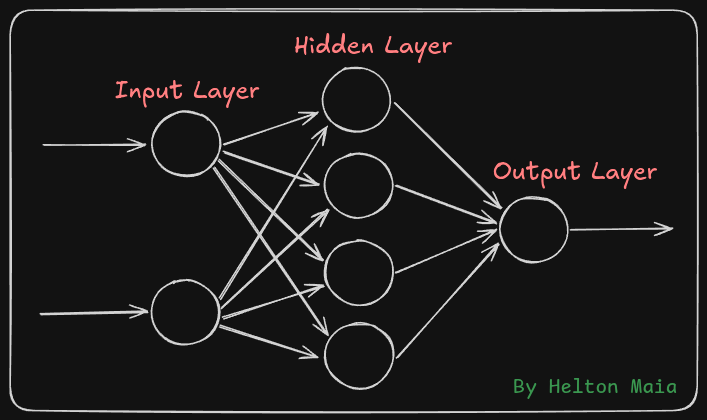
Camada de Entrada (Input Layer): Onde os dados brutos entram na rede, como os pixels de uma imagem.
Camadas Ocultas (Hidden Layers): Responsáveis por realizar transformações complexas nos dados, extraindo padrões relevantes por meio de cálculos e funções de ativação.
Camada de Saída (Output Layer): Produz a resposta final da rede, como a classe prevista para uma imagem.
A seguir, veja a estrutura de uma rede neural simples:
Múltiplos Neurônios e Camadas em Redes Neurais#
Depois de entender como um único neurônio funciona — somando entradas ponderadas e aplicando uma função de ativação — podemos evoluir para redes com múltiplos neurônios organizados em camadas densamente conectadas (fully connected layers). Ao empilhar essas camadas, a rede é capaz de aprender padrões cada vez mais complexos, fundamentais para tarefas como o reconhecimento de dígitos manuscritos.
Vamos utilizar o famoso conjunto de dados MNIST Digits, que contém imagens de 28x28 pixels representando dígitos de 0 a 9 escritos à mão.
Como a rede processa essas imagens?
Camada de Entrada: Cada imagem 28×28 contém 784 pixels. Esses valores (em tons de cinza entre 0 e 255) são geralmente normalizados para o intervalo [0, 1], o que facilita o treinamento da rede.
Primeira Camada Oculta: Supondo 128 neurônios, cada um realiza uma combinação linear dos 784 valores de entrada, seguida de uma função de ativação (como ReLU). Isso gera 128 ativações que representam padrões iniciais.
Segunda Camada Oculta: Com 64 neurônios, ela processa as ativações anteriores para extrair padrões mais abstratos, como contornos, formas e estruturas típicas de cada dígito.
Camada de Saída: Possui 10 neurônios, um para cada classe (dígitos de 0 a 9). Utiliza a função softmax para produzir probabilidades associadas a cada classe. A classe com maior probabilidade é a predição da rede.
Durante o treinamento, os pesos da rede são ajustados para minimizar o erro entre a saída prevista e a resposta correta. Isso é feito através do algoritmo de retropropagação do erro (backpropagation) e um otimizador (como o gradiente descendente).
Implementando Redes Neurais com Keras e TensorFlow#
Com a API Keras, integrada ao TensorFlow, é possível montar e treinar redes neurais de forma simples e eficiente. Veja abaixo um exemplo usando o clássico conjunto de dados MNIST, que contém imagens de dígitos manuscritos (0 a 9).
Importações, Dados e Normalização
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Input, Flatten, Dense
from tensorflow.keras.optimizers import Adam
# Carrega o dataset MNIST
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Normaliza os dados para o intervalo [0, 1]
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0
Arquitetura da Rede Neural
model = Sequential([
Input(shape=(28, 28)),
Flatten(),
Dense(128, activation='relu'),
Dense(64, activation='relu'),
Dense(10, activation='softmax')
])
Explicando cada camada:
Input(shape=(28, 28)): define o formato das imagens de entrada (28x28 pixels).Flatten(): transforma a imagem 2D em um vetor 1D com 784 valores (28 × 28), necessário para conectar à camada densa.Dense(128, activation='relu'): primeira camada oculta com 128 neurônios. A função ReLU (Rectified Linear Unit) permite que apenas valores positivos sejam ativados, acelerando o aprendizado.Dense(64, activation='relu'): segunda camada oculta com 64 neurônios, permitindo a aprendizagem de representações mais complexas.Dense(10, activation='softmax'): camada de saída com 10 neurônios, um para cada classe. A função softmax transforma os valores em probabilidades, que somam 1.
Compilando o Modelo
model.compile(optimizer=Adam(),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
optimizer='adam': define o algoritmo usado para atualizar os pesos.O Adam combina gradiente descendente com momentum e adaptação da taxa de aprendizado.
loss='sparse_categorical_crossentropy': mede o erro entre a saída da rede e a resposta correta.Usamos essa função porque os rótulos são inteiros (0 a 9), e não vetores one-hot.
metrics=['accuracy']: define acurácia como métrica de desempenho, isto é, a proporção de acertos da rede.
Treinamento do Modelo
model.fit(x_train, y_train, epochs=5)
O método
fit()realiza o treinamento da rede:A rede passa por 5 épocas (iterações completas sobre o conjunto de treino).
Os pesos são ajustados com base no erro observado.
O backpropagation é aplicado a cada lote de dados, ajustando os pesos para melhorar as previsões.
Avaliação do Modelo
test_loss, test_acc = model.evaluate(x_test, y_test)
print(f"Precisão no teste: {test_acc:.2%}")
evaluate()calcula a perda e a acurácia nos dados de teste (não vistos durante o treino).Serve como uma estimativa de generalização do modelo para dados reais.
Visualização de Amostras e Inferência
Visualizando dados de treino:
plt.figure(figsize=(10, 2))
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.imshow(x_train[i], cmap='gray')
plt.title(f"Label: {y_train[i]}")
plt.axis('off')
plt.suptitle("Amostras do Conjunto de Treino")
plt.show()
Inferência com imagens de teste:
# Faz inferência com as 10 primeiras imagens de teste
predictions = model.predict(x_test[:10])
plt.figure(figsize=(10, 2))
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.imshow(x_test[i], cmap='gray')
pred_label = np.argmax(predictions[i])
true_label = y_test[i]
plt.title(f"P:{pred_label}\nT:{true_label}", fontsize=8)
plt.axis('off')
plt.suptitle("Inferência: P = Previsto, T = Verdadeiro")
plt.show()
Matriz de Confusão
A matriz de confusão mostra, para cada classe verdadeira, como o modelo classificou as amostras. É uma excelente ferramenta para avaliar o desempenho detalhado do classificador.
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# Gera previsões para o conjunto de teste
y_pred = model.predict(x_test)
y_pred_labels = np.argmax(y_pred, axis=1)
# Gera a matriz de confusão
cm = confusion_matrix(y_test, y_pred_labels)
# Exibe a matriz graficamente
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=range(10))
disp.plot(cmap=plt.cm.Blues, xticks_rotation=45)
plt.title("Matriz de Confusão - MNIST")
plt.show()
Explicação
confusion_matrix(y_true, y_pred): compara os rótulos verdadeiros com os previstos.Diagonal principal: acertos (previsão == verdadeiro).
Fora da diagonal: erros (confusões entre dígitos).
Com o
ConfusionMatrixDisplay, o gráfico mostra claramente quais dígitos estão sendo confundidos, por exemplo, se o modelo costuma confundir o 4 com o 9.
Exercício Prático: Classificação de Imagens com o Dataset Fashion MNIST#
Neste exercício, você vai implementar e treinar sua própria rede neural para classificar imagens de roupas utilizando o conjunto de dados Fashion MNIST, com a API Sequential do Keras (TensorFlow).
O Fashion MNIST contém imagens em tons de cinza com resolução 28x28 pixels, organizadas em 10 categorias de roupas como camisetas, vestidos, tênis, bolsas, entre outros. É um dos datasets mais utilizados para aprendizado e experimentação com redes neurais simples.
Você deve começar carregando o dataset com tf.keras.datasets.fashion_mnist.load_data() e separando os dados de treino e teste (x_train, y_train, x_test, y_test). Em seguida, normalize as imagens dividindo os valores dos pixels por 255, para que os dados fiquem no intervalo entre 0 e 1.
Visualize algumas imagens de treino para entender melhor o conteúdo do conjunto de dados. Você pode usar o seguinte código para isso:
import matplotlib.pyplot as plt
import numpy as np
from tensorflow.keras.datasets import fashion_mnist
# Carrega o conjunto de dados Fashion MNIST
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
# Rótulos das classes
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
# Normaliza os pixels para o intervalo [0, 1]
x_train, x_test = x_train / 255.0, x_test / 255.0
# Exibe 10 imagens de treino com seus respectivos rótulos
plt.figure(figsize=(10, 2))
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.imshow(x_train[i], cmap='gray')
plt.title(class_names[y_train[i]], fontsize=8)
plt.axis('off')
plt.suptitle("Amostras do Fashion MNIST")
plt.show()
Depois disso, implemente uma rede neural com a API Sequential. Você poderá escolher:
Quantas camadas ocultas usar
Quantos neurônios em cada camada
Quais funções de ativação utilizar (como
relu,sigmoid,tanh)
A camada de saída deve conter 10 neurônios com ativação softmax, correspondentes às 10 categorias de roupas.
Compile o modelo com a função de perda sparse_categorical_crossentropy e a métrica accuracy. Experimente pelo menos dois otimizadores entre os seguintes e compare seus desempenhos:
adamsgdrmspropadagrad
Treine seu modelo com model.fit() por no mínimo 5 épocas. Observe e anote os valores de perda e acurácia durante o treinamento.
Depois do treinamento, avalie o desempenho do modelo no conjunto de teste usando model.evaluate() e imprima a acurácia final. Compare os resultados obtidos com cada otimizador testado.
Para entender melhor onde o modelo acerta ou erra, gere uma matriz de confusão. Você pode usar o código abaixo:
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# Previsões no conjunto de teste
y_pred = model.predict(x_test)
y_pred_labels = np.argmax(y_pred, axis=1)
# Matriz de confusão
cm = confusion_matrix(y_test, y_pred_labels)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=class_names)
disp.plot(cmap=plt.cm.Blues, xticks_rotation=45)
plt.title("Matriz de Confusão - Fashion MNIST")
plt.show()
Como tarefa adicional, monte um gráfico comparando a acurácia e a função de perda ao longo das épocas para cada otimizador. Isso ajudará a visualizar e justificar qual otimizador teve melhor desempenho em termos de velocidade de aprendizado e precisão final.