Capítulo 2: Processamento de Imagens

Capítulo 2: Processamento de Imagens#

cover

Técnicas para o Pré-processamento de Imagens#

O pré-processamento de imagens é uma etapa essencial em muitas aplicações de visão computacional. Consiste na aplicação de técnicas para melhorar a qualidade da imagem, remover ruídos e prepará-la para etapas posteriores de análise. Como destacam Gonzalez e Woods (2018), entre os métodos mais utilizados destaca-se a normalização, que padroniza características visuais para facilitar o processamento.

Normalização#

Objetivos da Normalização A normalização ajusta e padroniza as propriedades de uma imagem, tornando-a mais adequada para análise. Segundo Gonzalez e Woods (2018), suas principais vantagens incluem:

  • Melhoria da Qualidade: Corrige distorções, ajusta o contraste e remove ruídos, aumentando a precisão de análises posteriores.

  • Padronização: Garante consistência em conjuntos de imagens, facilitando comparações.

  • Eficiência em Algoritmos: Técnicas de visão computacional, como detecção de bordas e reconhecimento de padrões, dependem de imagens pré-processadas para melhor desempenho.

  • Redução de Ruído: Minimiza interferências (como variações de iluminação ou artefatos) que poderiam comprometer os resultados.

Técnicas de Normalização#

Diversas técnicas podem ser aplicadas, dependendo do objetivo e do tipo de imagem. As mais comuns são:

Equalização de Histograma Como descrevem Gonzalez e Woods (2018), esta técnica redistribui os níveis de intensidade da imagem para maximizar o contraste, destacando detalhes antes pouco visíveis. É particularmente útil em imagens com baixa variação tonal.

Filtros Espaciais Aplicados diretamente nos pixels da imagem para suavizar ou remover ruídos. Incluem:

  • Filtro de Média: Reduz ruídos, mas pode borrar detalhes.

  • Filtro de Mediana: Eficaz contra ruídos do tipo sal e pimenta.

  • Filtro Gaussiano: Suaviza a imagem preservando melhor as bordas.

Transformadas de Fourier Convertem a imagem para o domínio da frequência, permitindo a remoção de ruídos periódicos ou padrões indesejados (GONZALEZ; WOODS, 2018).

Normalização de Cores Ajusta as cores da imagem para corrigir variações de iluminação ou balanço de branco, sendo essencial em aplicações como reconhecimento facial.

Normalização de Intensidade Mapeia os valores de pixel para uma escala padronizada (ex.: [0, 1] ou [-1, 1]), garantindo consistência para algoritmos de aprendizado de máquina.

Normalização de Tamanho Redimensiona imagens para dimensões fixas, sendo crucial em redes neurais convolucionais (CNNs), onde todas as entradas devem ter o mesmo tamanho.

Normalização de Histograma Ajusta a distribuição de intensidades para seguir um padrão específico, facilitando a comparação entre diferentes imagens (GONZALEZ; WOODS, 2018).

Primeiro Exemplo de Normalização#

Normalização de Intensidade

Vamos começar com o exemplo mais básico de normalização — a normalização de intensidade, que ajusta os valores dos pixels para uma faixa específica. Este é um excelente ponto de partida para entender o pré-processamento de imagens.

Definição Matemática

A normalização min-max transforma cada valor \(x\) para um novo valor \(x'\) no intervalo desejado, geralmente \([0, 1]\), usando a fórmula:

\[ x' = \frac{x - x_{\text{min}}}{x_{\text{max}} - x_{\text{min}}} \]

  • \(x\) é o valor original do pixel;

  • \(x_{\text{min}}\) e \(x_{\text{max}}\) são os valores mínimo e máximo da imagem;

  • \(x'\) será o valor normalizado no intervalo \([0, 1]\).

No caso de imagens em 8 bits, é comum usar diretamente:

\[ x' = \frac{x}{255} \]

pois os valores de \(x\) estão entre 0 e 255.

Exemplo Prático: Normalizando para [0, 1]

O código abaixo demonstra como normalizar uma imagem em tons de cinza para o intervalo \([0, 1]\) usando Python e OpenCV:

Imagem Original: Sun

import matplotlib.pyplot as plt
import numpy as np

# Carregar a imagem
img = plt.imread('sun.jpeg')

# Converter para escala de cinza
if img.ndim == 3:
    img_gray = img[..., :3].mean(axis=2)  # Média dos canais RGB (ignora alpha)
else:
    img_gray = img  # Já está em grayscale

# Normalizar diretamente para [0, 1]
if img_gray.max() > 1.0:  # Se os valores estiverem em [0, 255]
    img_normalizada = img_gray.astype('float32') / 255.0
else:  # Se já estiver em [0, 1]
    img_normalizada = img_gray.astype('float32')

# Exibir resultados
plt.figure(figsize=(12, 6))

# Subplot para imagem original (em escala de cinza)
plt.subplot(1, 2, 1)
plt.imshow(img_gray, cmap='gray', vmin=0, vmax=255 if img_gray.max() > 1.0 else 1)
plt.title(f'Imagem Original\n(0-{"255" if img_gray.max() > 1.0 else "1"})')
plt.axis('off')

# Subplot para imagem normalizada
plt.subplot(1, 2, 2)
plt.imshow(img_normalizada, cmap='gray', vmin=0, vmax=1)
plt.title('Imagem Normalizada\n(0.0-1.0)')
plt.axis('off')

plt.tight_layout()
plt.show()

# Valores mínimos/máximos
print(f"Original - Min: {img_gray.min()}, Max: {img_gray.max()}")
print(f"Normalizada - Min: {img_normalizada.min():.4f}, Max: {img_normalizada.max():.4f}")

Por que normalizar para [0, 1]?

  • Padronização: Todos os pixels estarão na mesma escala

  • Compatibilidade: Muitos algoritmos de ML esperam valores nesse intervalo

  • Estabilidade numérica: Reduz problemas com overflow/underflow em cálculos

  • Facilidade de visualização: Valores entre 0 e 1 são intuitivos

Podemos também normalizar cada canal (R, G, B) separadamente para manter a imagem colorida normalizada, o que preserva a relação entre as cores originais.

📝 Exercício: Normalização de Imagem Colorida por Canal RGB#

Objetivo: Aprender a normalizar imagens coloridas considerando as características individuais de cada canal de cor.

Tarefa:

  • Carregar uma imagem colorida em formato JPEG ou PNG

  • Separar a imagem em seus três canais de cor: Vermelho (R), Verde (G) e Azul (B)

  • Observar que cada canal possui seus próprios valores mínimo e máximo de intensidade

  • Normalizar cada canal individualmente para o intervalo [0, 1], onde:

    • O valor 0 corresponde à intensidade mínima encontrada no canal

    • O valor 1 corresponde à intensidade máxima encontrada no canal

  • Recombinar os três canais normalizados para obter a imagem colorida final

Resultado Esperado. Uma nova versão da imagem onde:

  • Cada pixel em cada canal terá valores entre 0 e 1

  • A aparência visual original será mantida

  • As proporções entre os canais serão preservadas

  • A distribuição de intensidades em cada canal estará normalizada

📌 Importante
Lembre-se que a normalização deve considerar os valores extremos específicos de cada canal, pois podem variar entre os canais R, G e B.

Histograma de Imagens#

Um histograma de imagem é uma representação gráfica que descreve a distribuição das intensidades dos pixels. Ele indica quantos pixels possuem cada valor de intensidade — normalmente de 0 a 255 em imagens de 8 bits.

Definição Matemática

O histograma de uma imagem digital é uma função discreta representada por:

\[ H(k) = n_k \quad \text{para} \quad k \in [0, L-1] \]

Onde:

  • \(L\) é o número de níveis de intensidade possíveis (tipicamente \(L = 256\) para imagens de 8 bits);

  • \(n_k\) é o número de pixels com intensidade igual a \(k\);

  • \(N\) é o número total de pixels na imagem: \(N = \sum_{k=0}^{L-1} n_k\)

A versão normalizada do histograma, interpretada como uma função de probabilidade, é dada por:

\[ P(k) = \frac{H(k)}{N} \]

Tabela: Interpretação de Histogramas#

Característica

Comportamento no Histograma

Interpretação

Exemplo Prático

Ajuste Sugerido

Distribuição

Picos agudos

Grandes áreas com tons uniformes (ex: céu, paredes)

Céu azul sem nuvens

Aplicar texturas ou variações tonais

Vales profundos

Falta de pixels na faixa tonal (pode indicar falta de detalhes)

Transições bruscas entre objetos

Suavizar transições ou equalizar histograma

Contraste

Amplo (0-255)

Boa distribuição tonal - imagem com alto contraste

Cenas bem iluminadas com sombras definidas

Manter como referência

Estreito (<50% da escala)

Baixo contraste - tons concentrados em faixa limitada

Neblina ou fotos em condições de baixa luz

Equalização ou ajuste de curvas

Cortado nos extremos

Perda de informação (clipping) em sombras ou altas-luzes

Reflexos em água ou sol direto

Reduzir exposição ou usar HDR

Exposição

Deslocado à esquerda (0-127)

Subexposição - detalhes escuros perdidos

Fotografia noturna mal exposta

Aumentar brilho ou sombras

Deslocado à direita (128-255)

Superexposição - áreas estouradas (highlight clipping)

Neve ou cenas muito claras

Reduzir brilho ou recuperar altas-luzes

Curva balanceada (~128)

Exposição equilibrada - detalhes visíveis em sombras e altas-luzes

Retrato em luz difusa

Ideal - nenhuma correção necessária

Casos Especiais

Bimodal

Cena com dois grupos tonais dominantes (ex: objeto claro em fundo escuro)

Silhuetas contra o céo

Avaliar se é efeito desejado

Multimodal

Vários objetos com tons distintos (ex: cena com múltiplos elementos coloridos)

Natureza com flores coloridas

Processamento por regiões

Calculando o Histograma Para Imagem em Escala de Cinza:

import numpy as np
import matplotlib.pyplot as plt

# Carrega a imagem
img = plt.imread('sun.jpeg')

# Converte para escala de cinza, se for colorida (com 3 canais RGB)
if img.ndim == 3: 
    img = img.mean(axis=2)  # Faz a média dos 3 canais (R, G, B)

# Normaliza para faixa [0, 1] se os valores estiverem acima de 1
if img.max() > 1.0: 
    img = img / 255.0  # Normaliza dividindo por 255

# Calcula o histograma usando NumPy (agora com range [0, 1])
hist, bins = np.histogram(img, bins=256, range=(0, 1))

# Visualização da imagem e do histograma
fig, axes = plt.subplots(1, 2, figsize=(12, 5))

# Exibe a imagem em tons de cinza (agora com vmax=1)
axes[0].imshow(img, cmap='gray', vmin=0, vmax=1)
axes[0].axis('off')
axes[0].set_title('Imagem em Escala de Cinza')

# Plota o histograma de intensidades
axes[1].plot(bins[:-1], hist, color='black')  # bins[:-1] para alinhar com os valores de hist
axes[1].set_title('Distribuição de Intensidades')
axes[1].set_xlabel('Valor do Pixel (0 a 1)')
axes[1].set_ylabel('Frequência')

plt.tight_layout()
plt.show()

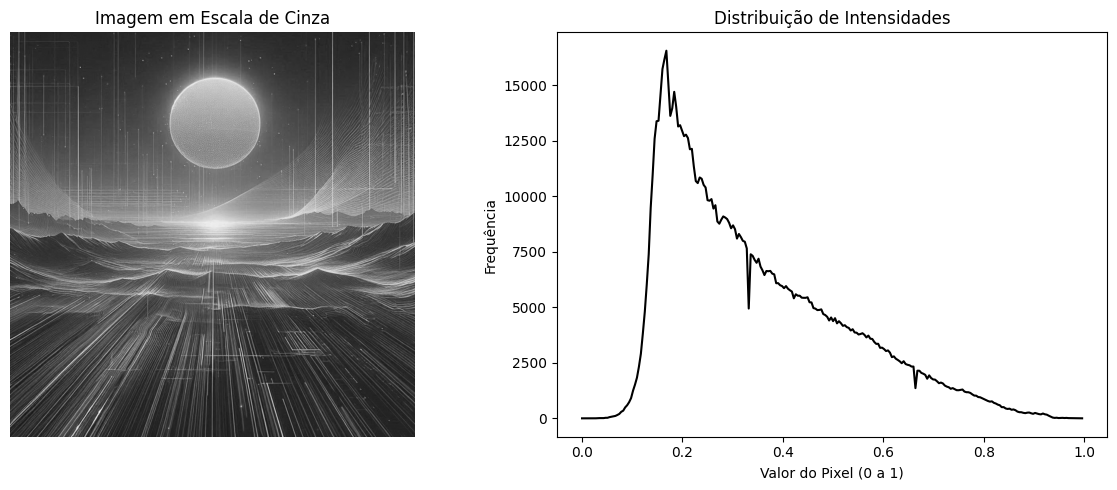
A função np.histogram calcula a distribuição dos níveis de intensidade da imagem, retornando dois arrays:

  • hist: o número de pixels em cada faixa de intensidade (ou bin);

  • bins: os valores que delimitam cada faixa (inclusive o limite superior final).

hist, bins = np.histogram(img, bins=256, range=(0, 256))

Você pode usar plt.plot() para uma linha ou plt.bar() para barras verticais:

plt.plot(bins[:-1], hist, color='black')  # bins[:-1] para alinhar com hist

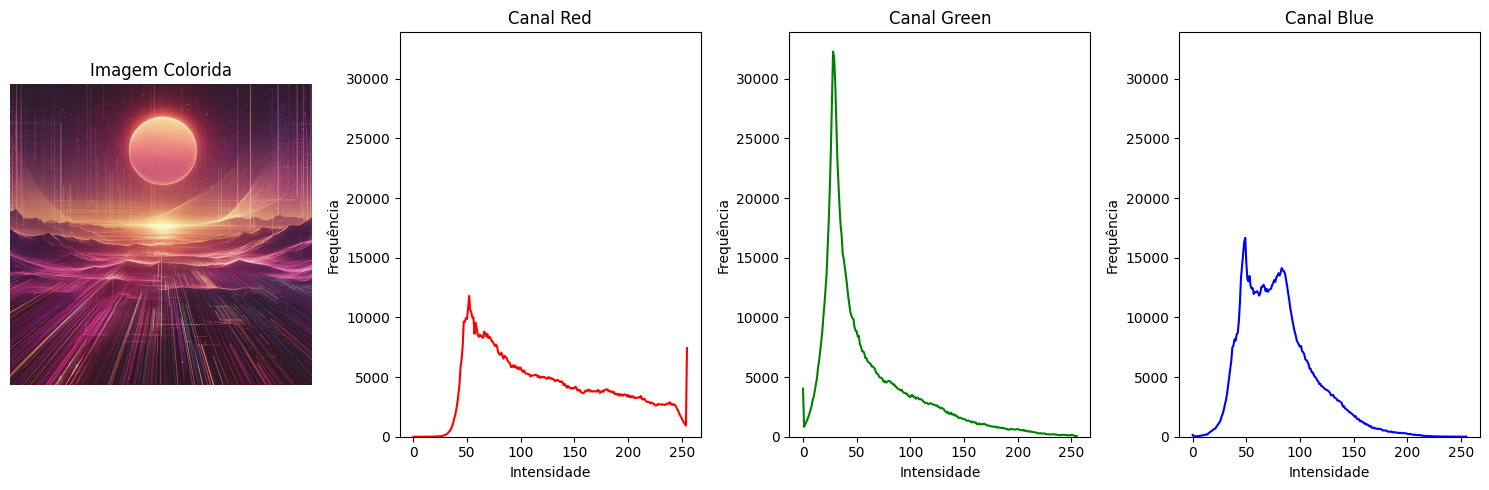
Para Imagem Colorida (RGB):

import numpy as np
import matplotlib.pyplot as plt

# Carrega a imagem colorida
img_color = plt.imread('sun.jpeg')

# Normaliza para [0, 1] se os valores estiverem acima de 1
if img_color.max() > 1.0:
    img_color = img_color / 255.0

# Calcula os histogramas dos canais e armazena os máximos
colors = ('red', 'green', 'blue')
hist_list = []
max_freq = 0

for i in range(3):
    canal = img_color[..., i].ravel()  # equivalente a img_color[:, :, i].ravel()
    hist, bins = np.histogram(canal, bins=256, range=(0, 1))
    hist_list.append((hist, bins))
    max_freq = max(max_freq, hist.max())  # Atualiza o maior valor de frequência

# Plotagem
plt.figure(figsize=(15, 5))

# Imagem original (agora mostrando com vmax=1)
plt.subplot(141)
plt.imshow(img_color, vmin=0, vmax=1)
plt.axis('off')
plt.title('Imagem Colorida')

# Histogramas dos canais com mesma escala no eixo Y
for i, color in enumerate(colors):
    hist, bins = hist_list[i]    
    plt.subplot(142 + i)
    plt.plot(bins[:-1], hist, color=color)
    plt.ylim(0, max_freq * 1.05)  # Limite ajustado com margem de 5%
    plt.title(f'Canal {color.title()}')
    plt.xlabel('Intensidade (0 a 1)')
    plt.ylabel('Frequência')

plt.tight_layout()
plt.show()

Equalização de Histograma#

Conceito Básico
A equalização de histograma é uma transformação não-linear que redistribui os valores de intensidade de uma imagem para maximizar seu contraste global. O método se baseia na estatística dos pixels para criar uma transformação adaptativa.

Matemática da Equalização

1. Função de Distribuição Cumulativa (CDF):

A CDF (Cumulative Distribution Function) representa a probabilidade acumulada de ocorrência dos níveis de intensidade:

\[ \text{CDF}(r_k) = \sum_{i=0}^{k} \frac{n_i}{N} \]

Onde:

  • \( n_i \) = número de pixels com intensidade \( i \)

  • \( N \) = número total de pixels (altura × largura)

  • \( r_k \) = nível de intensidade (de 0 a \(L-1 \))

Essa função indica a fração de pixels com intensidade menor ou igual a \( r_k \).

2. Transformação de Equalização:

A transformação que realiza a equalização é:

\[ s_k = T(r_k) = \text{round}\left( (L-1) \cdot \text{CDF}(r_k) \right) \]

Onde:

  • \( r_k \) é o valor original de intensidade de um pixel.

  • \( \text{CDF}(r_k) \) calcula a fração acumulada de pixels com intensidade até \( r_k \).

  • Multiplicamos essa fração por \( L - 1 \)) (valor máximo da faixa de intensidade) para escalar o resultado ao intervalo de saída.

  • O resultado é arredondado para garantir que o novo valor \( s_k \) seja um número inteiro válido.

Essa transformação redistribui os valores de intensidade com base na frequência acumulada, de forma que regiões de baixa variação ganhem mais contraste e a faixa dinâmica da imagem seja melhor aproveitada.

Propriedades Chave:

  • Preserva a ordem dos níveis de intensidade

  • É uma função monotonicamente crescente

  • Mapeia \( [0, L-1] \) \(\rightarrow [0, L-1] \)

3. Normalização do CDF:

Na prática, normalizamos a CDF para garantir o uso completo da faixa de intensidades, especialmente quando os níveis mais baixos não aparecem na imagem:

\[ \text{CDF}_{\text{norm}}(r_k) = \frac{\text{CDF}(r_k) - \text{CDF}_{\text{min}}}{1 - \text{CDF}_{\text{min}}} \]

Onde \( \text{CDF}_{\text{min}} \) é o menor valor não-zero da CDF.

Implementação Comparativa

import numpy as np
import cv2
import matplotlib.pyplot as plt

def detailed_histogram_equalization(img, L=256):
    """Implementação didática com todas as etapas matemáticas"""
    # Passo 1: Calcular histograma
    hist = np.bincount(img.flatten(), minlength=L)
    
    # Passo 2: Calcular PMF e CDF
    pmf = hist / hist.sum()  # Função massa de probabilidade
    cdf = np.cumsum(pmf)     # Função distribuição cumulativa
    
    # Passo 3: Normalização do CDF
    cdf_min = cdf[hist > 0][0]  # Primeiro valor não-zero
    cdf_norm = (cdf - cdf_min) / (1 - cdf_min)
    
    # Passo 4: Aplicar transformação
    transformed = np.round((L-1) * cdf_norm).astype(np.uint8)
    
    # Passo 5: Mapear pixels
    return transformed[img]

# Pipeline completo de análise
img_original = cv2.imread('sun.jpeg', cv2.IMREAD_GRAYSCALE)

# Versões processadas
img_numpy = detailed_histogram_equalization(img_original)
img_opencv = cv2.equalizeHist(img_original)

# Análise comparativa
plt.figure(figsize=(15, 10))

# Visualização das imagens
for i, (title, img) in enumerate(zip(
    ['Original', 'NumPy Equalization', 'OpenCV Equalization'],
    [img_original, img_numpy, img_opencv]
)):
    plt.subplot(2, 3, i+1)
    plt.imshow(img, cmap='gray', vmin=0, vmax=255)
    plt.title(title)
    plt.axis('off')

# Visualização dos histogramas
for i, (title, img, color) in enumerate(zip(
    ['Histograma Original', 'Histograma NumPy', 'Histograma OpenCV'],
    [img_original, img_numpy, img_opencv],
    ['red', 'green', 'blue']
)):
    plt.subplot(2, 3, i+4)
    plt.hist(img.ravel(), bins=256, range=[0,256], color=color)
    plt.title(title)
    plt.xlabel('Intensidade')
    plt.ylabel('Frequência')

plt.tight_layout()
plt.show()

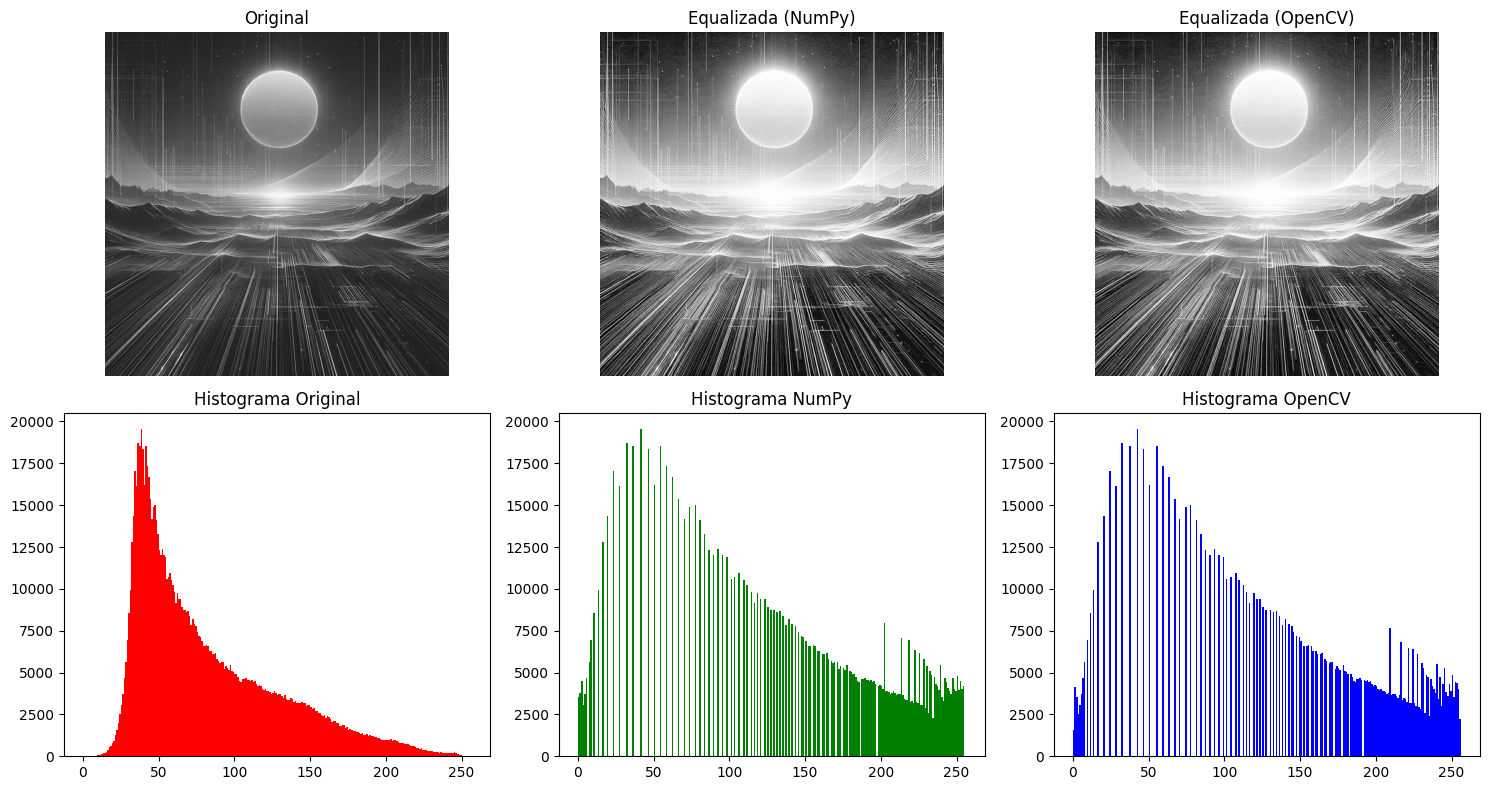
Figura: Resultado da equalização mostrando a expansão do histograma e melhoria de contraste. O método preserva os detalhes estruturais enquanto redistribui as intensidades.

📝 Exercício: Equalização de Histograma em Imagens Coloridas#

Implemente um pipeline de processamento de imagens coloridas com as seguintes etapas:

  • Leitura da Imagem

    • Carregue uma imagem JPEG ou PNG e normalize os pixels se necessário.

  • Histogramas RGB (Pré-equalização)

    • Calcule e plote os histogramas dos canais R, G e B, usando cores correspondentes.

  • Equalização por Canal

    • Equalize cada canal (R, G, B) separadamente com OpenCV, preservando as cores.

  • Visualização dos Resultados

    • Mostre a imagem original e a equalizada lado a lado.

    • Exiba os histogramas antes e depois da equalização, organizados em subplots.

  • Análise

    • Compare as distribuições antes e depois:

      • A equalização tornou os histogramas mais uniformes?

      • Alguma perda de informação ou artefato visual foi introduzida?

Desafio:

Implemente a equalização de histograma para vídeos coloridos.

  • Objetivo: aplicar a equalização de histograma a cada quadro (frame) de um vídeo.

  • Passos sugeridos:

    • Leia o vídeo usando cv2.VideoCapture.

    • Para cada frame, aplique o mesmo pipeline de equalização por canal.

    • Salve o vídeo final usando cv2.VideoWriter.

  • Dica: Certifique-se de manter o mesmo fps e dimensões do vídeo original.

Download dos Arquivos

Convolução de Imagens#

A convolução (vid) é uma operação matemática central no processamento digital de imagens. Seu principal objetivo é extrair e realçar características relevantes — como bordas, texturas, contornos ou regiões homogêneas — ao combinar uma imagem com um kernel (ou filtro). O resultado é uma nova imagem, cujas propriedades visuais são modificadas de acordo com a estrutura do kernel utilizado.

Matemática da Convolução#

Para imagens digitais, representadas como matrizes bidimensionais de pixels, a convolução discreta é definida por:

\[ (f * g)[x,y] = \sum_{i=-k}^{k} \sum_{j=-k}^{k} f[x-i,y-j] \cdot g[i,j] \]

Onde:

  • \(f\): Matriz da imagem original (dimensão M×N)

  • \(g\): Kernel ou filtro (dimensão K×K, com K ímpar, como 3×3 ou 5×5)

  • \((x,y)\): Coordenadas do pixel na imagem de saída

  • \(k\): Metade do tamanho do kernel, ou seja, \((K-1)/2\), necessário para centralizar o kernel sobre o pixel atual

Esse processo é repetido para cada pixel da imagem, levando em conta a vizinhança local e os coeficientes definidos pelo kernel.

Kernels: O Coração da Convolução#

Os kernels são pequenas matrizes de pesos que determinam como os valores dos pixels vizinhos devem ser combinados para gerar um novo valor. Suas propriedades determinam o tipo de transformação que será aplicada à imagem.

  • Dimensões Ímpares
    Garantem que o kernel tenha um centro bem definido para alinhar ao pixel sendo processado.

  • Normalização e Balanceamento
    Preserva o brilho da imagem (soma dos pesos = 1) ou enfatiza transições com pesos positivos e negativos.

  • Direcionalidade e Gradientes
    Detectam variações horizontais, verticais ou diagonais — úteis para encontrar bordas.

  • Objetivo Específico
    Cada kernel serve a uma tarefa: suavizar, realçar, detectar ruído, etc.

  • Localidade e Paralelismo
    Operação local e independente — ideal para paralelismo em GPUs e redes neurais convolucionais.

Exemplo de Kernel de Detecção de Bordas (Sobel Vertical):#

\[\begin{split} \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} \end{split}\]

Esse kernel detecta bordas verticais ao responder a variações horizontais na imagem. Parece um pouco abstrato mas entederemos em seguida.

Convolução Passo a Passo: Suavização com Filtro de Média#

Suponha uma imagem 5×5 e um kernel de média 3×3. A janela do kernel percorre a imagem, realizando multiplicações ponto a ponto seguidas de uma soma.

Matriz Original (Imagem A):

\[\begin{split} \begin{bmatrix} 10 & 20 & 30 & 40 & 50 \\ 20 & \boxed{30} & \boxed{40} & \boxed{50} & 60 \\ 30 & \boxed{40} & \boxed{50} & \boxed{60} & 70 \\ 40 & \boxed{50} & \boxed{60} & \boxed{70} & 80 \\ 50 & 60 & 70 & 80 & 90 \end{bmatrix} \end{split}\]

Submatriz usada na convolução:

\[\begin{split} \boxed{ \begin{bmatrix} 30 & 40 & 50 \\ 40 & 50 & 60 \\ 50 & 60 & 70 \end{bmatrix} } \end{split}\]

Kernel de Média (B):

\[\begin{split} \frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \end{split}\]

Convolução - exemplo de uma etapa:#

\[ \frac{1}{9}(30 + 40 + 50 + 40 + 50 + 60 + 50 + 60 + 70) = 50 \]

Efeitos de Borda e Estratégias de Padding#

Durante a convolução, nas bordas da imagem faltam vizinhos para o kernel. Para corrigir isso, se for de interesse, usamos técnicas de padding.

Modos Comuns de Padding#

Modo

Descrição

Efeito na Tamanho da Imagem

valid

Sem preenchimento

Reduz a imagem

same

Preenchimento com zeros

Mantém o tamanho original

reflect

Espelha os valores da borda

Mantém ou quase mantém o tamanho

replicate

Repete o valor do pixel da borda

Semelhante ao reflect

Cálculo da Dimensão de Saída#

Seja:

  • \(I\): tamanho da imagem original (largura ou altura)

  • \(K\): tamanho do kernel

  • \(P\): padding aplicado (pixels adicionados em cada lado)

  • \(S\): stride (passo da janela, geralmente 1)

A dimensão da imagem de saída será:

\[ O = \left\lfloor \frac{I - K + 2P}{S} \right\rfloor + 1 \]

Veja que:

  • valid: \(P = 0\) → a imagem encolhe

  • same: \(P = \left\lfloor \frac{K}{2} \right\rfloor\) → a imagem mantém tamanho

Exemplo — Modo valid (sem padding)

  • Imagem: \( I = 5 \)

  • Kernel: \( K = 3 \)

  • Padding: \( P = 0 \)

  • Stride: \( S = 1 \)

Aplicando na fórmula, temos:

\[ O = \left\lfloor \frac{5 - 3 + 2 \cdot 0}{1} \right\rfloor + 1 = \left\lfloor \frac{2}{1} \right\rfloor + 1 = 2 + 1 = 3 \]

Saída: 3×3

Exemplo — Modo same (padding para manter tamanho)

Para manter o tamanho \( O = I \), usamos:

\[ P = \left\lfloor \frac{K}{2} \right\rfloor \]

  • Imagem: \( I = 5 \)

  • Kernel: \( K = 3 \)

  • Stride: \( S = 1 \)

  • Padding: \( P = \left\lfloor \frac{3}{2} \right\rfloor = 1 \)

Aplicando:

\[ O = \left\lfloor \frac{5 - 3 + 2 \cdot 1}{1} \right\rfloor + 1 = \left\lfloor \frac{4}{1} \right\rfloor + 1 = 4 + 1 = 5 \]

Saída: 5×5 (mesma dimensão da imagem original)

Exemplo Visual: Comparação de Modos

Imagem Original (3×3):

\[\begin{split} \begin{bmatrix} 10 & 20 & 30 \\ 40 & 50 & 60 \\ 70 & 80 & 90 \end{bmatrix} \end{split}\]

Kernel (3×3):

\[\begin{split} \frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \end{split}\]

valid: apenas regiões totalmente dentro da imagem
Aplica o kernel apenas onde ele cabe por completo, por isso há redução no tamanho da saída.

\[ \begin{bmatrix} 50 \end{bmatrix} \]

same (com zero padding): mantém o tamanho da imagem

Para isso, adicionamos uma borda de zeros em volta da imagem original:

Imagem com padding zero:

\[\begin{split} \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 10 & 20 & 30 & 0 \\ 0 & 40 & 50 & 60 & 0 \\ 0 & 70 & 80 & 90 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{split}\]

A aplicação do kernel gera:

\[\begin{split} \begin{bmatrix} 13.3 & \cdots & 23.3 \\ \cdots & 50 & \cdots \\ 33.3 & \cdots & 43.3 \end{bmatrix} \end{split}\]

reflect (espelhamento das bordas):
As bordas são refletidas, evitando zeros e preservando mais o conteúdo da imagem.

\[\begin{split} \begin{bmatrix} 36.7 & \cdots & 43.3 \\ \cdots & 50 & \cdots \\ 46.7 & \cdots & 53.3 \end{bmatrix} \end{split}\]

Aplicações Práticas com Python#

Visualizando a Convolução

O código a seguir demonstra a convolução utilizando Python:

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve2d

# Define a matriz da imagem
A = np.array([[10, 20, 30, 40, 50],
              [20, 30, 40, 50, 60],
              [30, 40, 50, 60, 70],
              [40, 50, 60, 70, 80],
              [50, 60, 70, 80, 90]])

# Define o kernel de média
B = np.array([[1/9, 1/9, 1/9],
              [1/9, 1/9, 1/9],
              [1/9, 1/9, 1/9]])

# Realiza a convolução usando a função convolve2d do scipy
C = convolve2d(A, B, mode='valid')

# Subplots com aspect ratio
fig, axes = plt.subplots(1, 3, figsize=(16, 6), 
                         gridspec_kw={'width_ratios': [5, 3, 3]})  # Proporção dos tamanhos

# Imagem original
im1 = axes[0].imshow(A, cmap='gray', aspect='equal')
axes[0].set_title(f'Imagem Original ({A.shape[0]}x{A.shape[1]})')
#fig.colorbar(im1, ax=axes[0], fraction=0.046, pad=0.04)

# Kernel - respeitando a proporção
im2 = axes[1].imshow(B, cmap='gray', aspect='equal')
axes[1].set_title(f'Kernel ({B.shape[0]}x{B.shape[1]})')
axes[1].set_xticks([])  # Remove os valores do eixo x
axes[1].set_yticks([])  # Remove os valores do eixo y
#fig.colorbar(im2, ax=axes[1], fraction=0.046, pad=0.04)

# Imagem convolucionada
im3 = axes[2].imshow(C, cmap='gray', aspect='equal')
axes[2].set_title(f'Imagem Convolucionada ({C.shape[0]}x{C.shape[1]})')
axes[2].set_xticks([])  # Remove os valores do eixo x
axes[2].set_yticks([])  # Remove os valores do eixo y
#fig.colorbar(im3, ax=axes[2], fraction=0.046, pad=0.04)

plt.tight_layout()
plt.show()

Este código utiliza a função convolve2d da biblioteca scipy para realizar a convolução da matriz da imagem com o kernel de média. Ele exibe a imagem original, o kernel e a imagem resultante da convolução.

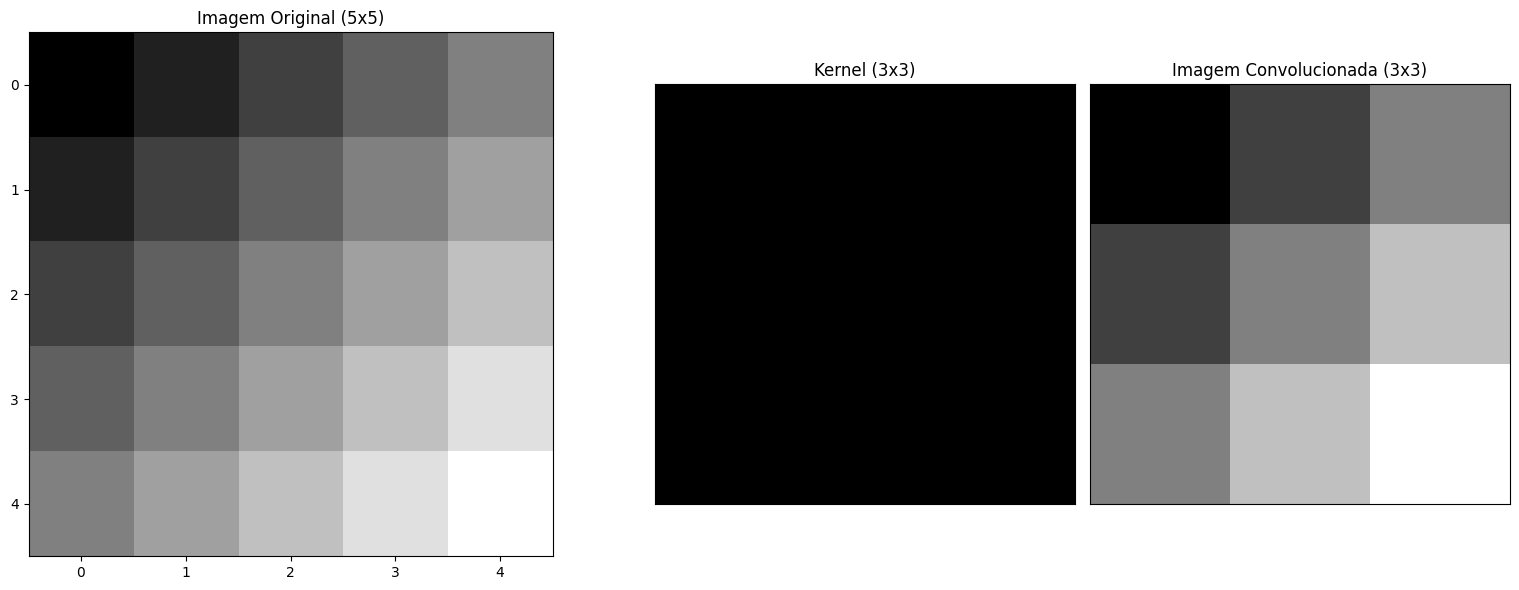
Exemplo de convolução

Vamos escolher uma imagem para realizar os testes a seguir.

🔹 Com OpenCV (Funções prontas e otimizadas)#

Suavização com Filtro Gaussiano

import cv2
import matplotlib.pyplot as plt

# Carrega a imagem
img = cv2.imread('bridge.jpeg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# Número de iterações do filtro Gaussiano
num_iterations = 5  # Altere conforme desejar

# Cria uma cópia da imagem para aplicar o filtro iterativamente
blurred_img = img.copy()

for _ in range(num_iterations):
    blurred_img = cv2.GaussianBlur(blurred_img, (5, 5), 0) #img, kernel, std

# Plota apenas a original e a última versão borrada
plt.figure(figsize=(10, 5))

plt.subplot(1, 2, 1)
plt.imshow(img)
plt.title("Imagem Original")
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(blurred_img)
plt.title(f"Filtro Gaussiano ({num_iterations}x)")
plt.axis('off')

plt.tight_layout()
plt.show()

Explicação:

  • cv2.GaussianBlur(src, ksize, sigmaX) aplica uma suavização com base em uma distribuição gaussiana.

    • src: imagem original.

    • ksize=(5,5): tamanho da máscara (kernel). Quanto maior, mais borrado o resultado.

    • sigmaX=0: o desvio padrão da Gaussiana. Zero permite que o OpenCV calcule automaticamente com base no tamanho do kernel.

  • Aqui, aplicamos o filtro várias vezes para reforçar o efeito.

  • Útil para remover ruídos leves e suavizar gradientes antes de aplicar detecção de bordas.

Detecção de Bordas com Sobel

import cv2
import numpy as np
import matplotlib.pyplot as plt

# Carrega a imagem original
img = cv2.imread('bridge.jpeg', cv2.IMREAD_GRAYSCALE)  # Sobel funciona melhor em tons de cinza

# Aplica Sobel nos dois eixos
sobel_x = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
sobel_y = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
sobel_combined = cv2.magnitude(sobel_x, sobel_y)

# Aplica Gaussiano DEPOIS (opcional para suavizar ruído nas bordas)
blurred_edges = cv2.GaussianBlur(sobel_combined, (5,5), 0)

# Plota os resultados
fig, axs = plt.subplots(1, 3, figsize=(15,5))
axs[0].imshow(img, cmap='gray')
axs[0].set_title("Original")
axs[0].axis('off')

axs[1].imshow(sobel_combined, cmap='gray')
axs[1].set_title("Sobel Puro")
axs[1].axis('off')

axs[2].imshow(blurred_edges, cmap='gray')
axs[2].set_title("Sobel + Gaussiano")
axs[2].axis('off')

plt.tight_layout()
plt.show()

Explicação:

  • cv2.Sobel(src, ddepth, dx, dy, ksize) calcula derivadas para encontrar bordas.

    • ddepth=cv2.CV_64F: profundidade dos dados de saída (64 bits flutuante para evitar perda de sinal negativo).

    • dx=1, dy=0: para detectar bordas horizontais (vice-versa para verticais).

    • ksize=3: tamanho do kernel de derivada.

  • cv2.magnitude(x, y) combina as bordas em X e Y para formar uma borda geral.

  • Aplicar o filtro Gaussiano depois ajuda a suavizar ruídos nas bordas detectadas.

Redução de Ruído com Filtro Mediano

import cv2
import numpy as np
import matplotlib.pyplot as plt

# Carregar imagem original
img = cv2.imread('bridge.jpeg')  # Substitua pelo seu arquivo
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# Adicionar ruído artificial (sal e pimenta)
def add_salt_pepper_noise(image, prob=0.05):
    output = np.copy(image)
    # Ruído sal (branco)
    salt = np.random.rand(*image.shape[:2]) < prob/2
    output[salt] = 255
    # Ruído pimenta (preto)
    pepper = np.random.rand(*image.shape[:2]) < prob/2
    output[pepper] = 0
    return output

noisy_img = add_salt_pepper_noise(img, prob=0.3)  # 30% de ruído

# Aplicar filtro mediano
median = cv2.medianBlur(noisy_img, 5)  # Kernel size 5 (deve ser ímpar)

# Visualização comparativa
fig, axs = plt.subplots(1, 2, figsize=(12, 6))

axs[0].imshow(noisy_img)
axs[0].set_title(f"Imagem com Ruído (30% sal-pimenta)")
axs[0].axis('off')

axs[1].imshow(median)
axs[1].set_title("Filtro Mediano (kernel=5)")
axs[1].axis('off')

plt.tight_layout()
plt.show()

Explicação:

  • cv2.medianBlur(src, ksize) aplica um filtro que substitui cada pixel pela mediana da vizinhança.

    • Muito eficaz contra ruídos do tipo sal e pimenta (pontinhos pretos e brancos aleatórios).

    • ksize deve ser ímpar (3, 5, 7…).

  • Aqui, um ruído artificial foi adicionado para mostrar a eficácia do filtro.

  • Dica: para preservar bordas, o filtro mediano é geralmente melhor que o Gaussiano.

🔹 Com NumPy (Definindo o Kernel Manualmente)#

Utilizando scipy.signal.convolve2d para aplicar filtros 2D com controle total, ideal para fins didáticos e experimentação com kernels personalizados.

Filtro de Média (Suavização Simples)

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve2d

# Carregar imagem em escala de cinza
img = plt.imread('bridge.jpeg')
img = img.mean(axis=2)  # Converter para escala de cinza

# Define o kernel de média (suavização simples)
kernel = np.ones((3, 3)) / 9

# Aplica a convolução
output = img.copy()

# num de convoluções
n = 10
for i in range(n):
    output = convolve2d(output, kernel, mode='same', boundary='fill', fillvalue=0)

# Visualização
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs[0].imshow(img, cmap='gray')
axs[0].set_title("Imagem Original (Gray)")
axs[0].axis('off')

axs[1].imshow(output, cmap='gray')
axs[1].set_title("Filtro de Média (3x3)")
axs[1].axis('off')

plt.tight_layout()
plt.show()

Explicação:

  • np.ones((3,3))/9 cria um kernel onde todos os elementos têm peso igual — média aritmética dos vizinhos.

  • convolve2d(img, kernel, mode='same', boundary='fill', fillvalue=0):

    • mode='same': saída com o mesmo tamanho da imagem original.

    • boundary='fill': bordas externas tratadas como zero.

  • Suaviza transições na imagem, útil para remover ruídos leves.

Detecção de Bordas com Filtro Laplaciano

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve2d

# Carregar imagem em escala de cinza
img = plt.imread('bridge.jpeg')
if img.ndim == 3:  # Se for colorida (RGB)
    img = img.mean(axis=2)  # Converter para escala de cinza

# Define o kernel Laplaciano
kernel = np.array([[0,  1, 0],
                   [1, -4, 1],
                   [0,  1, 0]])

# Aplica convolução
output = convolve2d(img, kernel, mode='same', boundary='fill', fillvalue=0)

# Pré-processamento para visualização
output_visual = np.abs(output)  # Valor absoluto para ver todas as bordas
output_visual = (output_visual - output_visual.min()) / (output_visual.max() - output_visual.min())  # Normaliza para [0,1]

# Visualização melhorada
fig, axs = plt.subplots(1, 3, figsize=(15, 5))

# Imagem original
axs[0].imshow(img, cmap='gray')
axs[0].set_title("Imagem Original")
axs[0].axis('off')

# Resultado Laplaciano (valores brutos)
axs[1].imshow(output, cmap='seismic', vmin=-100, vmax=100)  # Cores: vermelho=negativo, azul=positivo
axs[1].set_title("Laplaciano (valores reais)")
axs[1].axis('off')

# Resultado Laplaciano (absoluto normalizado)
axs[2].imshow(output_visual, cmap='gray')
axs[2].set_title("Laplaciano (absoluto normalizado)")
axs[2].axis('off')

plt.tight_layout()
plt.show()

Explicação:

  • O kernel realça regiões com mudança brusca de intensidade (bordas).

  • O centro negativo e vizinhos positivos atuam como uma segunda derivada discreta.

  • Ideal para detectar bordas finas e simétricas.

CNNs#

Daqui a pouco estudaremos as CNNs (Convolução em Redes Neurais), é importante saber que os kernels são aprendidos automaticamente durante o treinamento. Cada camada convolucional extrai características específicas e cada vez mais complexas da imagem:

Camada

Tamanho do Kernel

Nº de Filtros

Função da Camada

1

3×3

32

Bordas e cores básicas

2

5×5

64

Padrões e texturas

3

3×3

128

Formas complexas e objetos

Esses filtros tornam possíveis aplicações como reconhecimento facial, análise médica, e detecção de objetos em tempo real.

📝 (Exercício Prático) ´Processamento de Vídeo com OpenCV#

Objetivo:
Aprender a carregar, modificar e salvar vídeos usando a biblioteca OpenCV.

Tarefas:

  • Carregar um vídeo (de arquivo ou webcam).

  • Converter cada frame para escala de cinza.

  • Salvar o vídeo processado em um novo arquivo.

Código Base (Passo a Passo):

import cv2

# 1. Carregar vídeo (substitua 'video.mp4' pelo seu arquivo ou use 0 para webcam)
cap = cv2.VideoCapture('video.mp4')

# Verifica se o vídeo foi carregado corretamente
if not cap.isOpened():
    print("Erro ao abrir o vídeo!")
    exit()

# 2. Obter propriedades do vídeo (largura, altura e FPS)
width = int(cap.get(cv2.CAP_PROP_FRAME_WIDTH))
height = int(cap.get(cv2.CAP_PROP_FRAME_HEIGHT))
fps = cap.get(cv2.CAP_PROP_FPS)

# 3. Criar o objeto de escrita do novo vídeo (grayscale)
output = cv2.VideoWriter('video_out.mp4',
                         cv2.VideoWriter_fourcc(*'mp4v'),  # Codec MP4
                         fps,
                         (width, height),
                         isColor=False)  # Vídeo em tons de cinza

# 4. Processar frame a frame, aplicar filtros, etc
# ...

# 5. Liberar recursos
cap.release()
output.release()
cv2.destroyAllWindows()

print("Vídeo processado e salvo como 'video_out.mp4'!")

Próximos Desafios (opcional):

  • Aplique equalização de histograma em cada frame antes de salvar.

  • Escolha e aplique um filtro (mediana, gaussiano, bordas etc).

  • Crie um vídeo que combine frames originais e processados lado a lado.

Desafio:

  • Criar um gerador de filtros adaptativo e especializado para CNNs. Falar com o professor!

🧠 Exercícios Conceituais#

1. Importância do Pré-processamento de Imagens Explique por que o pré-processamento é uma etapa essencial em projetos de visão computacional.

  • Quais problemas podem surgir ao utilizar imagens brutas sem pré-processamento?

  • Cite algumas técnicas comuns de pré-processamento e suas finalidades.

2. Normalização de Intensidade A normalização de intensidade ajusta os valores dos pixels para uma faixa específica.

  • Descreva como a normalização min-max transforma os valores de uma imagem.

  • Em quais situações essa técnica é particularmente útil?

3. Equalização de Histograma A equalização de histograma redistribui os níveis de intensidade para melhorar o contraste da imagem.

  • Como essa técnica pode realçar detalhes em imagens com baixa variação tonal?

  • Quais são as possíveis limitações da equalização de histograma?

4. Filtros Espaciais: Média, Mediana e Gaussiano Compare os filtros de média, mediana e Gaussiano em termos de suas aplicações e efeitos nas imagens.

  • Qual filtro seria mais adequado para remover ruídos do tipo “sal e pimenta”?

  • Em que casos o filtro Gaussiano é preferido?

5. Realce de Bordas em Imagens O realce de bordas é fundamental para destacar transições abruptas de intensidade.

  • Quais operadores são comumente utilizados para essa finalidade?

  • Como o realce de bordas contribui para a segmentação de objetos em uma imagem?

6. Redimensionamento de Imagens Redimensionar imagens para dimensões fixas é uma prática comum em redes neurais convolucionais (CNNs).

  • Quais são os desafios ao redimensionar imagens sem distorcer informações importantes?

  • Como o redimensionamento afeta o desempenho de modelos de aprendizado de máquina?

7. Convolução e Kernels A convolução é uma operação fundamental em processamento de imagens.

  • Explique como os kernels (ou filtros) são utilizados na convolução para detectar características específicas na imagem.

  • Dê exemplos de kernels comuns e suas aplicações.

8. Padding em Convoluções O padding é uma técnica utilizada para lidar com as bordas durante a convolução.

  • Quais são os tipos comuns de padding e como eles influenciam o resultado da convolução?

  • Por que o uso adequado de padding é importante em redes neurais convolucionais?

Referências e Conteúdo Extra#