Capítulo 7: Computação Numérica e Visualização de Dados

NumPy - Computação Numérica

NumPy é uma biblioteca fundamental para computação numérica em Python. Ela fornece ferramentas poderosas para manipulação eficiente de arrays multidimensionais e operações matemáticas rápidas. NumPy é amplamente utilizado em diversas áreas, desde ciência de dados até aprendizado de máquina.

Importando a Biblioteca NumPy

Para utilizar o NumPy, você precisa importar a biblioteca em seu código Python. A instrução import numpy as np é comumente usada para importar o NumPy e atribuir a ele o apelido “np”. Isso facilita a referência às funções e objetos da biblioteca.

import numpy as np

Definindo Arrays

A definição de arrays é um aspecto fundamental do NumPy. Você pode criar arrays unidimensionais (vetores) e multidimensionais (matrizes) de forma simples e eficiente.

# Criando um array unidimensional
array_1d = np.array([1, 2, 3, 4, 5])
print(f"array_1d:\n{array_1d}")

# Criando um array bidimensional
array_2d = np.array([[1, 2, 3], [4, 5, 6]])
print(f"array_2d:\n{array_2d}")

# Criando arrays especiais
zeros_array = np.zeros((3, 3))  # Array 3x3 preenchido com zeros
print(f"zeros_array:\n{zeros_array}")

ones_array = np.ones((2, 4))   # Array 2x4 preenchido com uns
print(f"ones_array:\n{ones_array}")

random_array = np.random.rand(3, 2)  # Array 3x2 com valores aleatórios entre 0 e 1
print(f"random_array:\n{random_array}")

Saída esperada do código:

array_1d:
[1 2 3 4 5]

array_2d:
[[1 2 3]
 [4 5 6]]

zeros_array:
[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

ones_array:
[[1. 1. 1. 1.]
 [1. 1. 1. 1.]]

random_array:
[[0.53719399 0.11460566]
 [0.54644121 0.10672048]
 [0.01692397 0.05397693]]

Nota: Os valores no random_array podem variar devido à geração aleatória.

Operações com Arrays (Vetorização)

A vetorização no NumPy refere-se ao processo de aplicar operações diretamente sobre arrays inteiros, sem a necessidade de escrever loops explícitos.

# Definindo arrays
array_1d = np.array([1, 2, 3, 4, 5])
array_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Soma de arrays
soma_arrays = array_1d + array_1d
print(f"Soma dos arrays:\n{soma_arrays}")

# Multiplicação de arrays
mult_arrays = array_1d * 3
print(f"Multiplicação dos arrays:\n{mult_arrays}")

# Produto escalar
prod_escalar = np.dot(array_1d, array_1d)
print(f"Produto escalar dos arrays:\n{prod_escalar}")

# Soma dos elementos de uma linha em uma matriz
soma_linha = np.sum(array_2d, axis=1)
print(f"Soma dos elementos de cada linha na matriz:\n{soma_linha}")

# Soma dos elementos de uma coluna em uma matriz
soma_coluna = np.sum(array_2d, axis=0)
print(f"Soma dos elementos de cada coluna na matriz:\n{soma_coluna}")

# Média dos elementos de uma linha em uma matriz
media_linha = np.mean(array_2d, axis=1)
print(f"Média dos elementos de cada linha na matriz:\n{media_linha}")

# Média dos elementos de uma coluna em uma matriz
media_coluna = np.mean(array_2d, axis=0)
print(f"Média dos elementos de cada coluna na matriz:\n{media_coluna}")

# Produto de duas matrizes
matriz_a = np.array([[1, 2], [3, 4]])
matriz_b = np.array([[5, 6], [7, 8]])
produto_matrizes = np.dot(matriz_a, matriz_b)
print(f"Produto das matrizes:\n{produto_matrizes}")

Saída do Código:

Soma dos arrays:
[2 4 6 8 10]

Multiplicação dos arrays:
[3 6 9 12 15]

Produto escalar dos arrays:
55

Soma dos elementos de cada linha na matriz:
[6 15 24]

Soma dos elementos de cada coluna na matriz:
[12 15 18]

Média dos elementos de cada linha na matriz:
[2. 5. 8.]

Média dos elementos de cada coluna na matriz:
[4. 5. 6.]

Produto das matrizes:
[[19 22]
 [43 50]]

Criando Arrays com Valores Específicos

O NumPy facilita a criação de arrays preenchidos com valores pré-definidos ou gerados automaticamente. Essa funcionalidade é particularmente útil para inicializar arrays em situações como geração de dados de teste, configurações de simulações e cálculos numéricos.

Arrays com Valores Espaçados Uniformemente

A função np.linspace(start, stop, num) gera um array unidimensional com valores igualmente espaçados entre os limites definidos (start e stop). O parâmetro num controla a quantidade de elementos no array.

Exemplo:

import numpy as np

# Array unidimensional com valores espaçados uniformemente
linear_array = np.linspace(0, 1, 5)  # Cria um array com 5 elementos de 0 a 1
print(f"Array linear:\n{linear_array}")

Saída do Código:

Array linear:
[0.   0.25 0.5  0.75 1.  ]

Arrays com Valores Repetidos

Outra função útil é np.full(shape, fill_value), que cria um array de qualquer dimensão com todos os elementos iguais a um valor específico. Isso é útil para inicializar matrizes com valores constantes.

Exemplo:

# Array 3x3 preenchido com o valor 7
full_array = np.full((3, 3), 7)
print(f"Array preenchido com valores constantes:\n{full_array}")

Saída do Código:

Array preenchido com valores constantes:
[[7 7 7]
 [7 7 7]
 [7 7 7]]

Comparação entre np.linspace e np.arange

Ambas as funções são úteis para criar arrays de forma eficiente, mas possuem finalidades diferentes:

• np.linspace: É mais adequado quando você deseja gerar um número específico de elementos, com valores espaçados uniformemente entre um intervalo.

• np.arange: É ideal quando você deseja controlar o passo (intervalo entre os valores) e não necessariamente o número total de elementos.

Exemplo Comparativo:

# Usando np.linspace para gerar 5 valores espaçados entre 0 e 1
linear_array = np.linspace(0, 1, 5)
print(f"Array gerado com np.linspace:\n{linear_array}")

# Usando np.arange para gerar valores de 0 a 5 com espaçamento de 1
arange_array = np.arange(0, 6, 1)
print(f"Array gerado com np.arange:\n{arange_array}")

Saída do Código:

Array gerado com np.linspace:
[0.   0.25 0.5  0.75 1.  ]

Array gerado com np.arange:
[0 1 2 3 4 5]

Quando Usar Cada Um?

• Use np.linspace quando:

  • Você sabe o número exato de pontos que deseja no array.

  • Precisa de valores espaçados uniformemente, independente do tamanho do passo.

• Use np.arange quando:

  • Você sabe o passo desejado e não se preocupa com o número total de elementos.

  • Está trabalhando com intervalos específicos e o espaçamento é fixo.

Concatenando e Empilhando Arrays

NumPy facilita a combinação de arrays usando funções de concatenação e empilhamento.

# Criando um array personalizado para empilhamento
custom_array = np.array([[10, 20, 30], [40, 50, 60]])

# Concatenando dois arrays unidimensionais
array_concatenada = np.concatenate((array_1d, linear_array))
print(f"Array concatenada:\n{array_concatenada}")

# Empilhando dois arrays bidimensionais verticalmente
stacked_array_vertical = np.vstack((array_2d, custom_array))
print(f"Array empilhada verticalmente:\n{stacked_array_vertical}")

# Empilhando dois arrays bidimensionais horizontalmente
stacked_array_horizontal = np.hstack((array_2d, custom_array))
print(f"Array empilhada horizontalmente:\n{stacked_array_horizontal}")

Saída do Código:

Array concatenada:
[1.   2.   3.   4.   5.   0.   0.25 0.5  0.75 1.  ]

Array empilhada verticalmente:
[[ 1  2  3]
 [ 4  5  6]
 [10 20 30]
 [40 50 60]]

Array empilhada horizontalmente:
[[ 1  2  3 10 20 30]
 [ 4  5  6 40 50 60]]

Reshape e Transposição

NumPy oferece ferramentas poderosas para reorganizar e manipular a estrutura dos arrays. Entre elas, destacam-se o reshape, para alterar a forma de um array, e a transposição, para reorganizar as dimensões de uma matriz.

Reshape: Alterando a Forma de um Array

A função reshape é usada para modificar a estrutura de um array, sem alterar os dados subjacentes. É útil para reorganizar arrays em diferentes dimensões.

• Requisitos: O número total de elementos deve permanecer o mesmo.

Exemplo: Transformar um array unidimensional (1D) em bidimensional (2D)

import numpy as np

# Alterando a forma de um array unidimensional para um array 5x1
array_1d = np.array([1, 2, 3, 4, 5])
array_novo_shape = array_1d.reshape((5, 1))
print(f"Array com novo shape (5x1):\n{array_novo_shape}")

Saída do Código:

Array com novo shape (5x1):
[[1]
 [2]
 [3]
 [4]
 [5]]

Exemplo: Converter um array bidimensional (3x3) em tridimensional (3x1x3)

# Alterando um array bidimensional para um array tridimensional
array_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
array_novo_shape_3d = array_2d.reshape((3, 1, 3))
print(f"Array com novo shape (3x1x3):\n{array_novo_shape_3d}")

Saída do Código:

Array com novo shape (3x1x3):
[[[1 2 3]]
 [[4 5 6]]
 [[7 8 9]]]

Transposição: Reorganizando as Dimensões

A transposição é usada para trocar linhas por colunas em arrays bidimensionais (ou reorganizar dimensões em arrays multidimensionais). No NumPy, isso é feito com o atributo .T.

Exemplo: Transpor um array bidimensional 3x2 para 2x3

# Transpondo um array bidimensional
array_2d = np.array([[1, 2, 3], [4, 5, 6]])
array_transposta = array_2d.T
print(f"Array transposta (2x3):\n{array_transposta}")

Saída do Código:

Array transposta (2x3):
[[1 4]
 [2 5]
 [3 6]]

Quando Usar Reshape e Transposição

• Reshape:

  • Reorganizar dados para compatibilidade com operações ou visualizações específicas.

  • Utilizado para preparar arrays para algoritmos que esperam formatos específicos.

• Transposição:

  • Reorganizar dimensões para análises de matrizes ou manipulações em álgebra linear.

  • Útil em casos onde as linhas precisam ser tratadas como colunas e vice-versa.

Funções Matemáticas

O NumPy oferece uma ampla gama de funções matemáticas otimizadas para operações com arrays. Abaixo estão algumas das funções mais comuns organizadas por categoria, seguidas de exemplos.

Tabela de Funções Matemáticas

Categoria	Função	Descrição
Trigonométricas	np.sin(array)	Calcula o seno de cada elemento do array.
	np.cos(array)	Calcula o cosseno de cada elemento do array.
	np.tan(array)	Calcula a tangente de cada elemento do array.
Exponenciais e Logarítmicas	np.exp(array)	Calcula o exponencial \( e^x \) de cada elemento.
	np.log(array)	Calcula o logaritmo natural \( \ln(x) \) de cada elemento.
Outras Funções	np.sqrt(array)	Calcula a raiz quadrada de cada elemento do array.

Funções Trigonométricas

As funções trigonométricas podem ser usadas para cálculos com ângulos, sendo que os valores devem ser ajustados para evitar resultados indefinidos.

Exemplo:

import numpy as np

# Ajustando os ângulos para evitar valores indefinidos
angle = np.array([0, np.pi/2 - 0.01, np.pi, 3*np.pi/2 + 0.01])

print(f"Seno: {[f'{x:.2f}' for x in np.sin(angle)]}")
print(f"Cosseno: {[f'{x:.2f}' for x in np.cos(angle)]}")
print(f"Tangente: {[f'{x:.2f}' for x in np.tan(angle)]}")

Saída do Código:

Seno: ['0.00', '1.00', '0.00', '-1.00']
Cosseno: ['1.00', '0.00', '-1.00', '0.00']
Tangente: ['0.00', '100.33', '-0.00', '-100.33']

Funções Exponenciais e Logarítmicas

As funções exponenciais e logarítmicas são amplamente utilizadas em cálculos matemáticos e científicos.

Exemplo:

import numpy as np

values = np.array([1, 2, 3, 4])
print(f"Exponencial: {[f'{x:.2f}' for x in np.exp(values)]}")
print(f"Logaritmo Natural: {[f'{x:.2f}' for x in np.log(values)]}")

Saída do Código:

Exponencial: ['2.72', '7.39', '20.09', '54.60']
Logaritmo Natural: ['0.00', '0.69', '1.10', '1.39']

Nota: O cálculo do logaritmo natural requer que os elementos do array sejam estritamente positivos. Caso contrário, ocorrerá um erro.

Raiz Quadrada

A função np.sqrt permite calcular a raiz quadrada de cada elemento de um array. Para lidar com números negativos, pode-se utilizar números complexos.

Exemplo:

import numpy as np

values = np.array([4, 9, 16, 25])
print(f"Raiz Quadrada: {[f'{x:.2f}' for x in np.sqrt(values)]}")

Saída do Código:

Raiz Quadrada: ['2.00', '3.00', '4.00', '5.00']

Dica: Para calcular a raiz quadrada de números negativos, considere usar números complexos ao especificar dtype=complex.

Operações Estatísticas

O NumPy oferece funções e recursos avançados para cálculos estatísticos, manipulação de dados e operações lógicas. Abaixo, as operações estão organizadas em categorias para facilitar o entendimento.

Tabela de Funções Estatísticas

Categoria	Função	Descrição
Média	np.mean(array)	Calcula a média aritmética do array.
Variância	np.var(array)	Calcula a variância, medindo a dispersão dos dados em relação à média.
Desvio Padrão	np.std(array)	Retorna a raiz quadrada da variância, indicando a dispersão dos dados na mesma unidade.
Mínimo e Máximo	np.min(array)	Retorna o menor valor do array.
	np.max(array)	Retorna o maior valor do array.

Exemplo Prático - Estatísticas

import numpy as np

# Array de exemplo
array = np.array([1, 2, 3, 4, 5])

# Cálculos estatísticos
media = np.mean(array)
variancia = np.var(array)
desvio_padrao = np.std(array)
minimo = np.min(array)
maximo = np.max(array)

# Exibição dos resultados
print(f"Média: {media:.2f}")
print(f"Variância: {variancia:.2f}")
print(f"Desvio Padrão: {desvio_padrao:.2f}")
print(f"Mínimo: {minimo}")
print(f"Máximo: {maximo}")

Saída do Código:

Média: 3.00
Variância: 2.00
Desvio Padrão: 1.41
Mínimo: 1
Máximo: 5

Tabela de Funções para Manipulação de Arrays

Categoria	Exemplo de Operação	Descrição
Indexação	array[1]	Acessa o elemento na posição 1 do array.
Fatiamento (Slicing)	array[1:4]	Retorna um subconjunto do array, do índice 1 ao 3 (exclui o 4).
Operações Lógicas	array[array > 3]	Retorna elementos do array que atendem à condição (maiores que 3).
	array[array > 3] = 0	Substitui valores maiores que 3 por zero.

Exemplo - Indexação e Fatiamento

# Criando um array de exemplo
array_1d = np.array([1, 2, 3, 4, 5])

# Acessando elementos específicos
elemento_2nd = array_1d[1]

# Fatiando (slicing) um array
slice_array = array_1d[1:4]

# Imprimindo os resultados
print("Elemento 2nd:", elemento_2nd)
print("Slice:", slice_array)

Saída do Código:

Elemento 2nd: 2
Slice: [2 3 4]

Exemplo - Operações Lógicas

# Criando um array de exemplo
array_1d = np.array([1, 2, 3, 4, 5])

# Filtrando elementos maiores que 3
array_filtrado = array_1d[array_1d > 3]

# Substituindo valores maiores que 3 por zero
array_1d[array_1d > 3] = 0

# Imprimindo os resultados
print("Array Filtrado:", array_filtrado)
print("Array 1D após substituição:", array_1d)

Saída do Código:

Array Filtrado: [4 5]
Array 1D após substituição: [1 2 3 0 0]

Trabalhando com Arquivos

O NumPy oferece funções simples e eficientes para salvar e carregar arrays. Essas ferramentas são essenciais para armazenar grandes volumes de dados numéricos ou compartilhar arrays entre diferentes programas.

Tabela de Funções para Manipulação de Arquivos

Função	Descrição
np.save	Salva um array NumPy em um arquivo binário no formato .npy.
np.load	Carrega um array salvo previamente no formato .npy.

Salvando Arrays com np.save

A função np.save permite salvar um array em um arquivo binário. O formato .npy garante a preservação da estrutura e do tipo de dados do array.

Exemplo Prático:

import numpy as np

# Criando um array
array_to_save = np.array([1, 2, 3, 4, 5])

# Salvando o array em um arquivo
np.save('array_salvo', array_to_save)

Após a execução, será gerado um arquivo chamado array_salvo.npy no diretório atual.

Carregando Arrays com np.load

A função np.load é usada para recuperar arrays previamente salvos. Isso é especialmente útil para reutilizar dados armazenados sem recriá-los manualmente.

Exemplo Prático:

import numpy as np

# Carregando o array salvo
loaded_array = np.load('array_salvo.npy')

# Exibindo o array carregado
print("Array Carregado:", loaded_array)

Saída do Código:

Array Carregado: [1 2 3 4 5]

Matplotlib - Visualização de Dados

Introdução ao Matplotlib

A visualização de dados é uma etapa crucial na análise e interpretação de informações complexas. Transformar dados brutos em representações visuais intuitivas facilita a identificação de padrões, tendências e a comunicação de resultados de forma clara e impactante. Nesse cenário, o Matplotlib se destaca como uma ferramenta essencial para profissionais e pesquisadores que trabalham com dados.

O que é Matplotlib?

O Matplotlib é uma biblioteca poderosa e versátil para visualização de dados em Python. Desenvolvida por John D. Hunter em 2003, tornou-se um padrão amplamente adotado na comunidade científica e de análise de dados. Sua combinação de simplicidade e capacidade de produzir gráficos de alta qualidade a torna ideal tanto para tarefas rápidas quanto para projetos mais complexos.

Por que usar o Matplotlib?

O Matplotlib se destaca pela sua flexibilidade e ampla integração com o ecossistema Python. Ele é capaz de atender tanto a necessidades simples, como gráficos rápidos para análise exploratória, quanto a demandas complexas, permitindo personalizações detalhadas. Além disso, sua integração perfeita com bibliotecas populares como NumPy, Pandas e SciPy oferece uma experiência fluida para quem trabalha com grandes volumes de dados.

Outro fator que reforça sua utilidade é a forte comunidade de usuários e desenvolvedores, que garante suporte contínuo e atualizações regulares. A biblioteca também possui uma documentação abrangente, tornando-a acessível até para iniciantes. Por fim, o Matplotlib permite exportar gráficos em diversos formatos, como PNG, PDF e SVG, o que o torna ideal para apresentações e publicações profissionais.

Funcionalidades e Personalização

Com o Matplotlib, é possível criar uma grande variedade de gráficos, incluindo linhas, dispersão, barras, histogramas, gráficos de pizza, boxplots, mapas de calor, gráficos 3D e muitos outros. O nível de personalização oferecido é um de seus maiores diferenciais: você pode controlar cores, estilos de linha, tamanhos de fonte, legendas, rótulos e até incluir anotações específicas.

Essa capacidade de ajuste detalhado permite criar visualizações que se alinham com padrões corporativos, acadêmicos ou simplesmente preferências estéticas, enriquecendo a comunicação visual.

Integração com o Ecossistema Python

O Matplotlib se integra perfeitamente com outras bibliotecas do ecossistema Python, potencializando suas funcionalidades. Ele funciona de forma natural com:

• NumPy, para cálculos numéricos eficientes;

• Pandas, para manipulação e análise de dados estruturados;

• Seaborn, para gráficos estatísticos mais estilizados;

• Scikit-learn, para visualização de resultados em aprendizado de máquina.

Essa integração amplia o alcance de suas aplicações, tornando-o uma ferramenta indispensável para cientistas de dados e analistas.

Um Exemplo Prático

Abaixo, um exemplo básico demonstra como criar um gráfico de linha utilizando o Matplotlib. Esse exemplo serve como ponto de partida para explorar as inúmeras possibilidades que a biblioteca oferece:

# Importando a biblioteca Matplotlib
import matplotlib.pyplot as plt

# Definindo os dados para os eixos X e Y
x = [1, 2, 3, 4, 5]
y = [2, 4, 6, 8, 10]

# Criando o gráfico de linha
plt.plot(x, y)

# Adicionando rótulo ao eixo X
plt.xlabel('Eixo X')

# Adicionando rótulo ao eixo Y
plt.ylabel('Eixo Y')

# Adicionando título ao gráfico
plt.title('Gráfico de Linha Simples')

# Exibindo o gráfico
plt.show()

Gráfico de Linha: Evolução de Casos de COVID-19 no Brasil

Este exemplo utiliza o Matplotlib para criar um gráfico de linha representando a evolução dos casos de COVID-19 no Brasil. A biblioteca NumPy é utilizada para gerar dados fictícios para ilustração.

# Importando as bibliotecas necessárias
import matplotlib.pyplot as plt  # Para criação de gráficos
import numpy as np  # Para operações numéricas e geração de dados aleatórios

# Gerando dados fictícios para ilustração
dias = np.arange(1, 31)  # Cria um array de 1 a 30, representando os dias do mês
casos_diarios = np.random.randint(100, 1000, size=30).cumsum()  # Gera números aleatórios entre 100 e 1000 para 30 dias e calcula a soma cumulativa

# Criando o gráfico de linha
plt.plot(dias, casos_diarios, 
         marker='o',  # Adiciona marcadores circulares nos pontos de dados
         linestyle='-',  # Define o estilo da linha como contínua
         color='b',  # Define a cor da linha como azul
         label='Casos Diários')  # Adiciona uma legenda para a linha

# Configurando os rótulos dos eixos e o título do gráfico
plt.xlabel('Dias')  # Rótulo para o eixo X
plt.ylabel('Total de Casos')  # Rótulo para o eixo Y
plt.title('Evolução de Casos de COVID-19 no Brasil')  # Título do gráfico

plt.legend()  # Exibe a legenda no gráfico

# Exibe o gráfico na tela
plt.show()

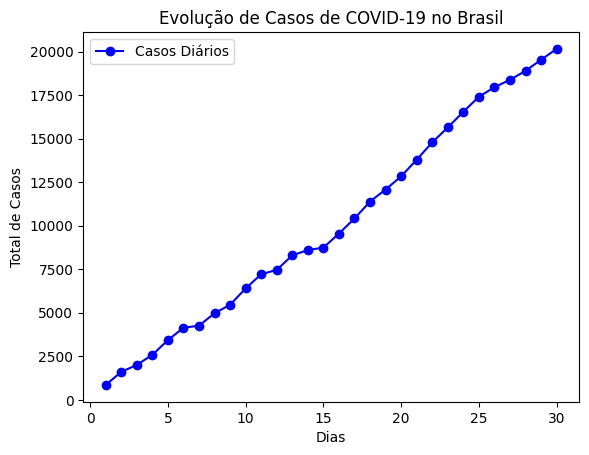
Gráfico de Barras: Distribuição de Renda no Brasil

Neste exemplo, um gráfico de barras é utilizado para representar a distribuição de renda no Brasil. Os dados são fictícios e representam percentuais da população em diferentes faixas de renda.

import matplotlib.pyplot as plt

# Dados fictícios para ilustração
faixas_renda = ['0-999', '1000-1999', '2000-2999', '3000-3999', '4000+']
percentuais = [20, 30, 25, 15, 10]

# Criando o gráfico de barras
plt.bar(faixas_renda, percentuais, color='green')

# Adicionando rótulos e título
plt.xlabel('Faixas de Renda')
plt.ylabel('Percentual da População')
plt.title('Distribuição de Renda no Brasil')

# Exibindo o gráfico
plt.show()

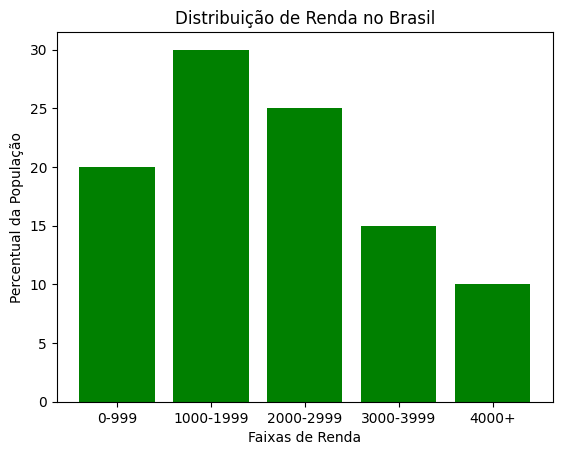
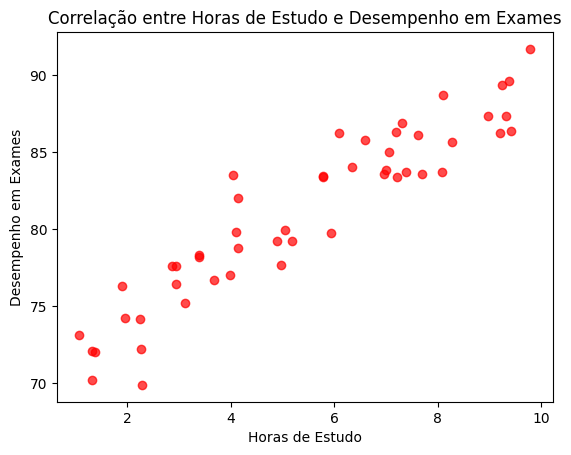
Gráfico de Dispersão: Correlação entre Duas Variáveis

Este exemplo utiliza um gráfico de dispersão para visualizar a correlação entre duas variáveis fictícias: horas de estudo e desempenho em provas.

import matplotlib.pyplot as plt
import numpy as np

# Dados fictícios para ilustração
horas_estudo = np.random.uniform(1, 10, size=50)
desempenho_exames = 70 + 2 * horas_estudo + np.random.normal(0, 2, size=50)

# Criando o gráfico de dispersão
plt.scatter(horas_estudo, desempenho_exames, color='red', alpha=0.7)

# Adicionando rótulos e título
plt.xlabel('Horas de Estudo')
plt.ylabel('Desempenho em Exames')
plt.title('Correlação entre Horas de Estudo e Desempenho em Exames')

# Exibindo o gráfico
plt.show()

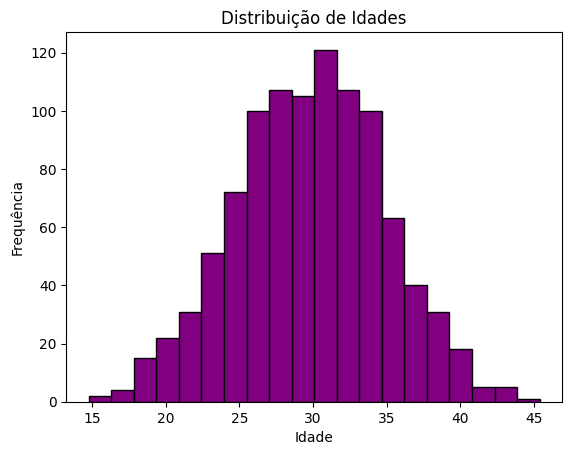
Histograma: Distribuição de uma Variável

Neste exemplo, um histograma é utilizado para representar a distribuição de idades em uma amostra de pessoas.

import matplotlib.pyplot as plt
import numpy as np

# Dados fictícios para ilustração
idades = np.random.normal(30, 5, size=1000)

# Criando o histograma
plt.hist(idades, bins=20, color='purple', edgecolor='black')

# Adicionando rótulos e título
plt.xlabel('Idade')
plt.ylabel('Frequência')
plt.title('Distribuição de Idades')

# Exibindo o gráfico
plt.show()

Trabalhando com Imagens

Matplotlib não é apenas para gráficos e plots; também é uma ferramenta poderosa para manipulação e visualização de imagens.

import matplotlib.pyplot as plt
import matplotlib.image as mpimg

# Define o caminho para a imagem local
caminho_imagem = "ch7.jpeg"  # Imagem na mesma pasta do arquivo .py

# Lê a imagem como um array numpy
img = mpimg.imread(caminho_imagem)

# Cria uma nova figura
plt.figure(figsize=(10, 8))

# Exibe a imagem
plt.imshow(img)

# Adiciona um título
plt.title("Minha Imagem Local")

# Remove os eixos
plt.axis('off')

# Mostra a figura
plt.show()

Salvando Gráficos como Figuras

A biblioteca Matplotlib oferece uma maneira descomplicada de salvar gráficos em diversos formatos, como PNG, PDF, SVG e JPEG. Como exemplo, vamos criar um scatter plot.

import matplotlib.pyplot as plt
import numpy as np

# Dados para o scatter plot
x = [1, 2, 3, 4, 5]
y = [2, 4, 6, 8, 10]

# Ajustar a cor e tamanho dos pontos com base nos valores de Y
colors = np.arange(len(y))
sizes = [40 * val for val in y]

# Criar um scatter plot personalizado
plt.scatter(x, y, c=colors, s=sizes, cmap='viridis', edgecolor='black', alpha=0.7, label='Pontos de Exemplo')
plt.colorbar(label='Valores de Y')
plt.xlabel('Eixo X')
plt.ylabel('Eixo Y')
plt.title('Scatter Plot Didático')

# Adicionar uma linha de tendência
plt.plot(x, np.poly1d(np.polyfit(x, y, 1))(x), color='orange', linestyle='--', label='Linha de Tendência')

# Adicionar legenda
plt.legend()

# Adicionar grade para melhor visualização
plt.grid(True)

# Salvar o scatter plot como arquivo PNG
plt.savefig('scatter_plot.png')

# Exibir o scatter plot
plt.show()

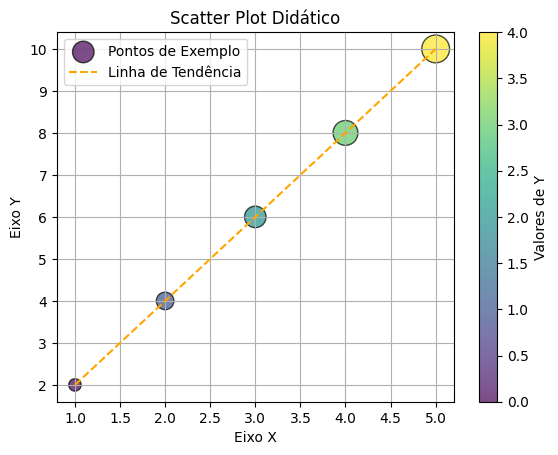
Para salvar, utilizamos a função savefig(), indicando o nome do arquivo com a extensão desejada. Para outros formatos, mude a extensão do nome:

plt.savefig('scatter_plot.pdf')
plt.savefig('scatter_plot.svg')
plt.savefig('scatter_plot.jpg')

A resolução padrão será utilizada, mas você pode ajustá-la conforme necessário com o argumento dpi. Este processo oferece uma maneira eficiente de preservar visualizações geradas em Python para uso futuro, compartilhamento ou inclusão em documentos e apresentações.

Exercícios

1. Analisando Coleta de Temperaturas

Você é um cientista de dados trabalhando em um conjunto de dados de temperaturas diárias coletadas ao longo de uma semana. As temperaturas foram registradas em graus Celsius e estão organizadas em um array NumPy.

Dados:

import numpy as np

temperaturas = np.array([
    [25.5, 26.1, 27.8, 28.3, 27.9, 26.8, 25.9],  # Domingo
    [24.8, 25.3, 26.5, 27.1, 26.7, 25.6, 24.9],  # Segunda
    [23.9, 24.5, 25.8, 26.4, 26.0, 24.9, 24.1],  # Terça
    [24.2, 24.8, 26.1, 26.7, 26.3, 25.2, 24.4],  # Quarta
    [25.1, 25.7, 27.0, 27.6, 27.2, 26.1, 25.3],  # Quinta
    [26.0, 26.6, 28.1, 28.7, 28.3, 27.2, 26.3],  # Sexta
    [25.4, 26.0, 27.5, 28.0, 27.6, 26.5, 25.7]   # Sábado
])

Suas tarefas são:

• Calcular a temperatura média diária da semana.

• Encontrar a temperatura máxima e mínima da semana.

• Calcular a diferença entre a temperatura máxima e mínima de cada dia da semana.

# Teste
Etrada: Considere os dados apresentados no enunciado
Saída:
Temperatura média diária da semana:
Dia 1: 26.90°C
Dia 2: 25.84°C
Dia 3: 25.09°C
Dia 4: 25.39°C
Dia 5: 26.29°C
Dia 6: 27.31°C
Dia 7: 26.67°C

Temperatura máxima da semana: 28.70°C
Temperatura mínima da semana: 23.90°C

Diferença entre temperatura máxima e mínima de cada dia:
Dia 1: 2.80°C
Dia 2: 2.30°C
Dia 3: 2.50°C
Dia 4: 2.50°C
Dia 5: 2.50°C
Dia 6: 2.70°C
Dia 7: 2.60°C

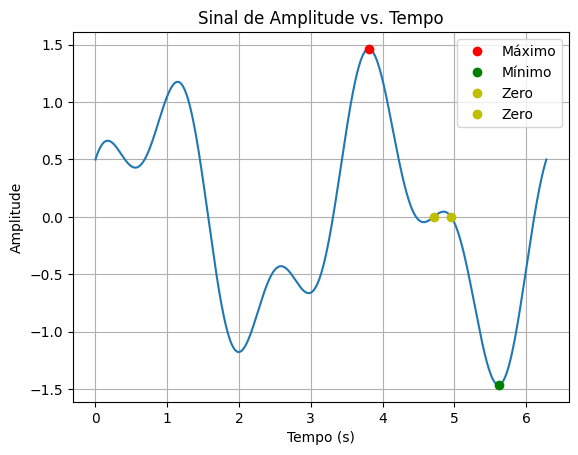
2. Análise de Ondas Sonoras

Você é um engenheiro de áudio trabalhando em um projeto de análise de ondas sonoras. Você tem um conjunto de dados que representa as amplitudes de uma onda sonora em diferentes pontos no tempo. Sua tarefa é analisar esses dados usando funções matemáticas do NumPy.

import numpy as np

# Dados: tempo em segundos e amplitudes correspondentes
tempo = np.linspace(0, 2*np.pi, 1000)
amplitudes = np.sin(2*tempo) + 0.5*np.cos(5*tempo)

Tarefas:

• Calcule o valor máximo e mínimo das amplitudes.

• Encontre os pontos de tempo onde a amplitude é próxima de zero (use np.where com np.isclose para considerar uma tolerância de atol=1e-3).

• Calcule a energia total do sinal (soma dos quadrados das amplitudes).

• Arredonde todos os resultados para 4 casas decimais e imprima os resultados de cada tarefa.

Opcionalmente, você pode plotar os gráficos utilizando o matplotlib para visualizar os resultados.

# Teste
Entrada: Utilize os dados apresentados no enunciado.
Saída:
Amplitude máxima: 1.4627
Amplitude mínima: -1.4628

Pontos de tempo onde a amplitude é próxima de zero:
4.7108 segundos
4.9561 segundos

Energia total do sinal: 624.6250

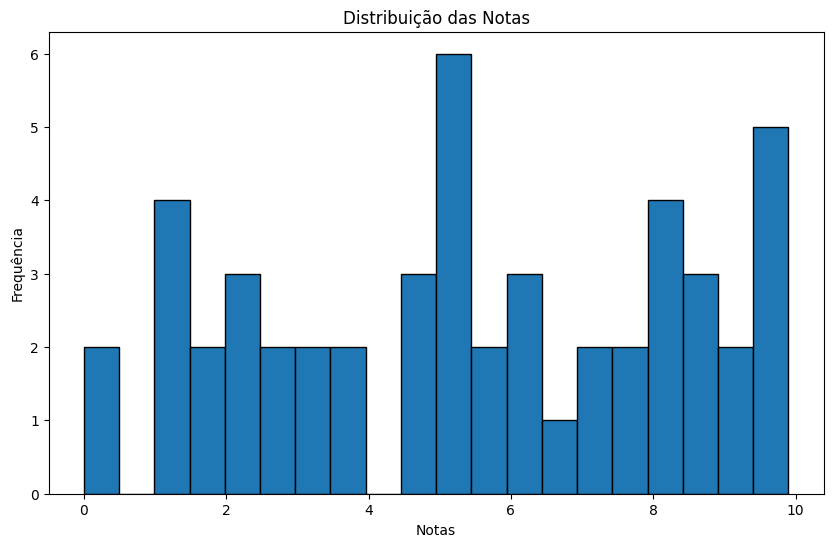
3. Cálculo de Médias e Desvios Padrão

Desenvolva um programa que analisa as notas de uma turma de alunos em uma disciplina. O objetivo é gerar um relatório estatístico básico que inclua a média, a variância e o desvio padrão das notas dos alunos.

Implemente uma função usando o NumPy para calcular as seguintes estatísticas:

• Média das notas: A média aritmética das notas.

• Variância das notas: A medida de dispersão que indica o quão espalhadas as notas estão em relação à média.

• Desvio padrão das notas: A raiz quadrada da variância, que fornece uma medida da dispersão das notas em relação à média.

Implemente uma outra função para imprimir o relatório final no seguinte formato:

• “Média das notas: X.XX”

• “Variância das notas: X.XX”

• “Desvio padrão das notas: X.XX”

Onde X.XX deve ser substituído pelos valores calculados, arredondados para duas casas decimais.

Opcionalmente, você pode plotar um histograma para visualizar a distribuição das notas usando a biblioteca matplotlib.

# Teste
Entrada:
6.3, 9.5, 1.7, 9.1, 8.2, 1.8, 0.4, 7.4, 4.6, 7.7, 8.1, 1.4, 3.8, 6.6, 7.6, 3.4, 3.8, 9.3, 9.9, 2.5, 6.3, 5.1, 5.4, 1.1, 4.5, 2.4, 8.7, 9.9, 2.0, 5.1, 8.0, 5.3, 1.0, 1.3, 8.5, 5.6, 4.7, 0.0, 6.0, 3.2, 2.2, 9.5, 9.7, 5.1, 5.6, 5.4, 8.7, 7.1, 2.6, 8.3
Saída:
Média: 5.43
Variância: 8.37
Desvio padrão: 2.89

4. Operações Algébricas em Matrizes

Neste exercício, você irá implementar operações algébricas fundamentais em matrizes utilizando a biblioteca NumPy. O objetivo é consolidar o entendimento sobre multiplicação, soma, transposição, inversão de matrizes e cálculo de determinantes.

Instruções

1. Geração das Matrizes

• Crie duas matrizes quadradas \(A\) e \(B\) de dimensões \(3 \times 3\), preenchidas com números inteiros aleatórios entre 1 e 10.

• Defina uma semente aleatória recebida como entrada para garantir a reprodutibilidade dos resultados. Utilize a função numpy.random.seed para configurar a semente, seguida por numpy.random.randint para gerar as matrizes.

2. Operações Algébricas

• a) Soma das Matrizes: Calcule a soma \(C = A + B\).

• b) Produto das Matrizes: Calcule o produto matricial \(D = A \cdot B\) (multiplicação matricial).

• c) Transposição: Encontre a transposta da matriz \(D\), denotada por \(D^T\).

• d) Determinante: Calcule o determinante de \(D\) utilizando numpy.linalg.det.

• e) Inversão de Matriz:

  • Verifique se \(D\) é invertível (determinante diferente de zero).

  • Se for, calcule sua inversa \(D^{-1}\) usando numpy.linalg.inv.

  • Caso contrário, informe que \(D\) não possui inversa.

3. Relatório Final Implemente uma função para exibir os resultados das operações em um relatório formatado da seguinte forma:

Relatório:

1. Matriz A: $

   (1)\[\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}\]

   $

2. Matriz B: (Formato semelhante ao de \(A\)).

3. Matriz C (A + B): Resultado da soma.

4. Matriz D (A \cdot B): Resultado da multiplicação matricial.

5. Matriz D Transposta: Resultado de \(D^T\).

6. Determinante de D: Valor do determinante.

7. Inversa de D: Mostre \(D^{-1}\) se existir, ou exiba “Matriz não invertível.”

Exemplo de Saída

# Teste com semente 42
Entrada:
   Matriz A:
   [[7, 4, 8],
    [5, 7, 3],
    [6, 9, 2]]

   Matriz B:
   [[6, 5, 2],
    [3, 5, 9],
    [6, 1, 1]]

Saída:
   Matriz C (A + B):
   [[13,  9, 10],
    [ 8, 12, 12],
    [12, 10,  3]]

   Matriz D (A * B):
   [[93, 79, 57],
    [81, 67, 44],
    [72, 57, 42]]

   Matriz D Transposta:
   [[93, 81, 72],
    [79, 67, 57],
    [57, 44, 42]]

   Determinante de D:
   -36.00000000000003

   Inversa de D:
   [[-0.5         0.33333333 -0.16666667],
    [ 0.25       -0.5         0.41666667],
    [ 0.125       0.16666667 -0.20833333]]

Dicas

• Utilize np.isclose para comparar o determinante com zero, evitando erros de precisão numérica.

• Teste o código com diferentes valores de semente para verificar a robustez da implementação.

• Utilize np.dot ou o operador @ para realizar a multiplicação matricial.