Capítulo 3: Análise e Filtragem de Sinais

A análise de sinais é um campo fascinante que envolve a decomposição de um sinal em suas componentes de frequência. Essa técnica permite que se compreendam como diferentes frequências contribuem para a formação do sinal total. Uma das ferramentas mais poderosas e amplamente utilizadas para essa análise é a Transformada de Fourier (TF).

A Transformada de Fourier é um método matemático que transforma um sinal do domínio do tempo para o domínio da frequência. Isso significa que, em vez de analisarmos como um sinal varia ao longo do tempo, podemos examinar as frequências que compõem o sinal.

Transformada de Fourier Contínua

A Transformada de Fourier contínua lida com sinais contínuos no tempo, que podem assumir valores em qualquer instante. A equação matemática para a Transformada de Fourier contínua de um sinal x(t) é definida como:

(1)\[\begin{align} X(f) = \int_{-\infty}^{\infty} x(t) e^{-j2\pi ft}\, dt \end{align}\]

Nesta equação, \(X(f)\) representa a transformada de Fourier do sinal, \(x(t)\) é o sinal original no domínio do tempo, e a integral calcula a contribuição de todas as frequências possíveis. O termo \( e^{-j2\pi ft} \) é conhecido como função exponencial complexa e é fundamental na matemática das transformadas de Fourier.

Transformada de Fourier Discreta (DFT)

Na prática, muitos sinais que encontramos são discretos, por exemplo, nos computadores, o que significa que eles são amostrados em momentos específicos no tempo. Para lidar com esses sinais, utilizamos a Transformada de Fourier Discreta (DFT). A DFT é computada usando um algoritmo eficiente chamado Fast Fourier Transform (FFT), que reduz significativamente a complexidade computacional em comparação com a Transformada de Fourier Contínua. A equação para a DFT é a seguinte:

(2)\[\begin{align} X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N} \end{align}\]

Nesta equação, \(X[k]\) representa a transformada de Fourier discreta, \(x[n]\) são os valores amostrados do sinal, e \(N\) é o número de pontos no sinal. A DFT fornece uma representação das frequências discretas presentes no sinal amostrado.

Teorema de Nyquist

Um aspecto importante ao trabalhar com sinais discretos é o Teorema de Nyquist, que fornece diretrizes importantes para a amostragem adequada de sinais contínuos. O teorema afirma que, para reconstruir perfeitamente um sinal contínuo a partir de suas amostras discretas, a taxa de amostragem deve ser maior que o dobro da maior frequência presente no sinal. Matematicamente, o teorema pode ser expresso como:

(3)\[\begin{align} f_{amostragem} > 2 \cdot f_{máxima} \end{align}\]

Onde \(f_{amostragem}\) é a taxa de amostragem e \(f_{máxima}\) é a maior frequência presente no sinal. Se essa condição não for atendida, pode ocorrer um fenômeno conhecido como aliasing, resultando em distorção do sinal.

A Transformada de Fourier tem aplicações vastas e diversas. No processamento de áudio, é usada para análise de tons e harmônicos. No domínio das imagens, é essencial para compressão e filtragem. Em telecomunicações, facilita a modulação e demodulação de sinais. A Transformada de Fourier também encontra uso em áreas como processamento de sinais biológicos, análise de vibrações mecânicas e até mesmo em algoritmos de aprendizado de máquina.

Bibliotecas de software como NumPy, SciPy e Librosa em Python fornecem ferramentas poderosas e acessíveis para calcular e explorar transformadas de Fourier, tornando mais fácil do que nunca aplicar essas técnicas avançadas em projetos de processamento de sinais.

Calculando a Transformada de Fourier em Python

Vamos explorar o cálculo da Transformada de Fourier para diferentes tipos de sinais usando Python e algumas bibliotecas populares.

Onda Senoidal Simples

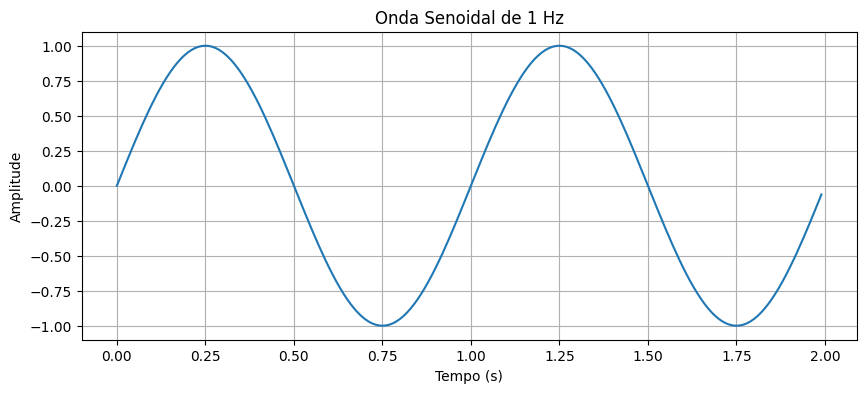
Primeiro, vamos gerar uma onda senoidal simples de 1 Hz e calcular sua FFT.

# Importando as bibliotecas
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq

# Parâmetros
f = 1  # frequência da onda em Hz
duration = 2  # duração total do sinal em segundos
sample_rate = 100  # taxa de amostragem em Hz

# Gerar um array com os instantes de tempo
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

# Gerar a onda senoidal
sine_wave = np.sin(2 * np.pi * f * t)

# Plotar a onda senoidal no domínio do tempo
plt.figure(figsize=(10, 4))
plt.plot(t, sine_wave)
plt.title('Onda Senoidal de 1 Hz')
plt.xlabel('Tempo (s)')
plt.ylabel('Amplitude')
plt.grid(True)
plt.show()

/home/hm/.local/lib/python3.10/site-packages/matplotlib/projections/__init__.py:63: UserWarning: Unable to import Axes3D. This may be due to multiple versions of Matplotlib being installed (e.g. as a system package and as a pip package). As a result, the 3D projection is not available.
  warnings.warn("Unable to import Axes3D. This may be due to multiple versions of "
/usr/lib/python3/dist-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.17.3 and <1.25.0 is required for this version of SciPy (detected version 1.26.3
  warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"

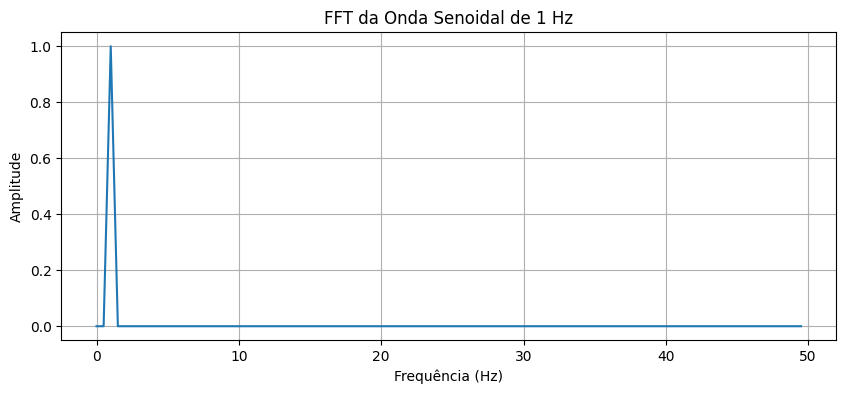
Agora, vamos calcular e plotar a FFT da onda senoidal:

# Função para calcular e plotar a FFT
def plot_fft(signal, title):
    N = len(signal)
    yf = fft(signal)
    xf = fftfreq(N, 1 / sample_rate)[:N//2]

    plt.figure(figsize=(10, 4))
    plt.plot(xf, 2.0/N * np.abs(yf[:N//2]))
    plt.title(title)
    plt.xlabel('Frequência (Hz)')
    plt.ylabel('Amplitude')
    plt.grid(True)
    plt.show()

# Plotar a FFT da onda senoidal
plot_fft(sine_wave, 'FFT da Onda Senoidal de 1 Hz')

Onda com Mistura de Sinais

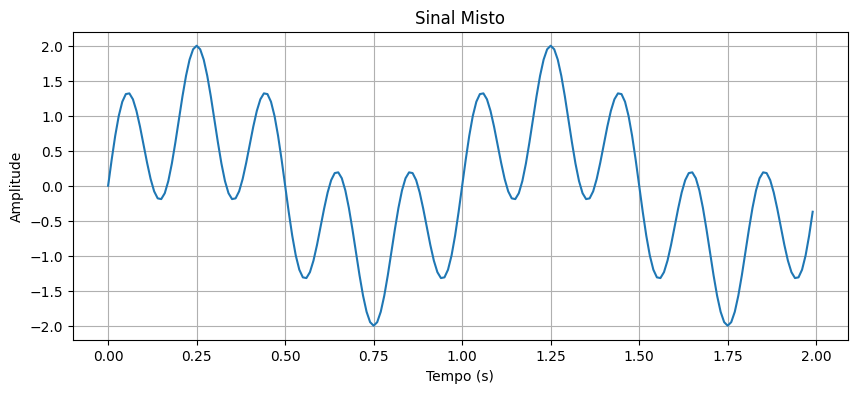
Agora, vamos criar um sinal mais complexo, que consiste em uma onda senoidal de 1 Hz e outra de 5 Hz, e então calcular sua FFT.

# Gerar a onda senoidal de 5 Hz
sine5hz = np.sin(2 * np.pi * 5 * t)

# Misturar as duas ondas senoidais
mixed_signal = sine_wave + sine5hz

# Plotar o sinal misto no domínio do tempo
plt.figure(figsize=(10, 4))
plt.plot(t, mixed_signal)
plt.title('Sinal Misto')
plt.xlabel('Tempo (s)')
plt.ylabel('Amplitude')
plt.grid(True)
plt.show()

# Plotar a FFT do sinal misto
plot_fft(mixed_signal, 'FFT do Sinal Misto')

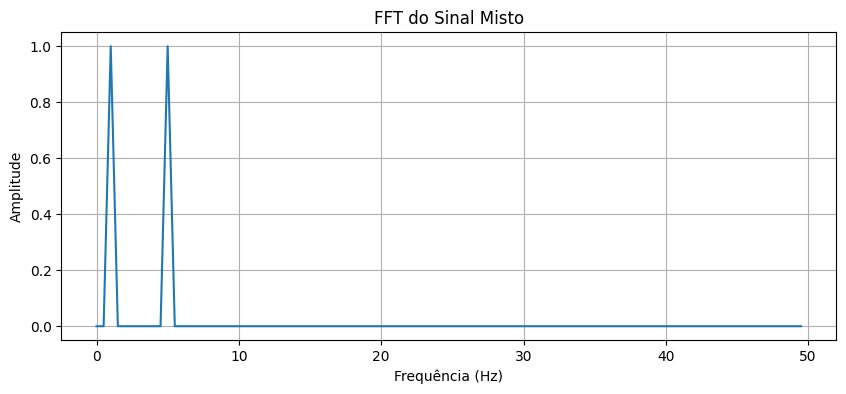
Espectrogramas

Um espectograma é uma representação visual que mostra como a frequência de um sinal varia com o tempo. Ele é útil para analisar sinais não estacionários, ou seja, sinais cuja frequência muda ao longo do tempo. Vamos usar a biblioteca scipy para calcular e plotar um espectograma.

Lendo Sinais Utilizando a Raspberry Pi Pico

O Raspberry Pi Pico é uma placa de desenvolvimento que oferece muitos recursos, incluindo a capacidade de ler sinais analógicos. Neste exemplo, demonstraremos como ler um sinal analógico usando o pino ADC (Conversor Analógico-Digital). Considere o código abaixo para leitura de um sinal.

from machine import Pin, ADC

# Configurar o pino ADC para entrada (escolha um pino, por exemplo, 26)
adc_pin = ADC(Pin(26))

# Ler o valor analógico do pino
valor_analogico = adc_pin.read_u16()

# Imprimir o valor analógico
print("Valor Analógico:", valor_analogico)

Neste código, primeiro importamos os módulos necessários, machine e ADC. Então, criamos um objeto ADC adc_pin e passamos o número do pino (neste caso, 26) como argumento para a classe Pin. Isto configura o pino especificado para conversão analógico-digital (ADC).

Em seguida, usamos o método read_u16() do objeto ADC para ler o valor analógico do pino especificado. Este método retorna um inteiro sem sinal de 16 bits representando o valor analógico.

Finalmente, imprimimos o valor analógico na console.

Filtragem de Sinais

• Circuitos para Filtragem

• Filtros de software

• Removendo 60HZ